数据结构

• 在本篇博文中，我将使用C语言/Cpp实现一些常见且重要的数据结构。我们将从最基础的顺序表和链表开始，逐步实现栈和队列，最后探讨树、二叉树以及堆的实现。

Part1：线性结构

1.1顺序表 📊

• 概念：顺序表是一种内存空间连续分布的线性表，分为静态和动态两种：
  • 静态顺序表：即普通数组，长度固定，需要给予初始长度，不支持空间的动态增长
  • 动态顺序表：支持空间动态增长的动态数组，可以通过重新分配更大的内存并复制旧数据来支持增长，C++中的vector的本质就是一个动态顺序表。
• ⚠️在下文中，我们讨论的顺序表指的就是动态顺序表

核心

// 导入需要使用的头文件
#include <stdio.h>
#include <stdlib.h>
// 定义数据类型别名，方便更改数据类型
typedef int SLDataType;

typedef struct SeqList
{
    SLDataType* _arr; // 🎯 数据存储区
    size_t _size;     // 📏 当前元素计数
    size_t _capacity; // 🏗️ 总容量
}SL; // 别名

// 以下为需要实现的函数的声明
void SeqListPrint(SL *sl);

// 构造与析构
void SeqListInit(SL* sl);
void SeqListDestroy(SL* sl);

// 增删查改
void SeqListPushBack(SL* sl, SLDataType x);
void SeqListPushFront(SL* sl, SLDataType x);
void SeqListPopBack(SL* sl);
void SeqListPopFront(SL* sl);

size_t SeqListFind(SL* sl, SLDataType x);
void SeqListInsert(SL* sl, size_t pos, SLDataType x);
void SeqListErase(SL* sl, size_t pos);

接口⚙️

构造与析构

• 初始化：
  • SeqListInit：用于给顺序表的每个成员一个初始值(指针类数据置为NULL，数值类数据置为0)，需要人为主动调用进行初始化，使用没有初始化的数据可能会引发异常
• 销毁：
  • SeqListDestroy：当顺序表不再需要使用时，将指定的顺序表销毁，需要人为主动调用进行销毁，不主动销毁就会造成内存泄漏

#pragma region 构造与析构
// 初始化
void SeqListInit(SL* sl)
{
    sl->_arr = NULL; // 初始值置为空
    sl->_size = sl->_capacity = 0;
}

// 销毁
void SeqListDestroy(SL* sl)
{
    if (sl->_arr != NULL)
    {
        free(sl->_arr);
        sl->_arr = NULL; // 置空,防止使用悬空指针
        sl->_size = sl->_capacity = 0;
    }
}
#pragma endregion

• 测试结果：这里我们的顺序表还是空的，所以Destroy函数不做测试

增删查改✂️

操作	函数	时间复杂度	说明
✅ 增	PushBack/PushFront	O(1)/O(N)	尾插高效，头插需移动元素
❌ 删	PopBack/PopFront	O(1)/O(N)	尾删高效，头删需移动元素
🔍 查	Find	O(N)	线性查找对应索引
✏️ 改	Insert/Erase	O(N)	指定位置操作

// 遍历
void SeqListPrint(SL* sl)
{
    for (int i = 0; i < sl->_size; i++)
    {
        printf("%d ", sl->_arr[i]);
    }
    printf("\n");
}

// 检查空间
static void SeqListCheckCapacity(SL* sl)
{
    if (sl->_size  sl->_capacity)
    {
        size_t newcapacity = sl->_capacity  0 ? 4 : 2 * sl->_capacity;
        SLDataType* tmp = (SLDataType*)realloc(sl->_arr, newcapacity * sizeof(SLDataType)); 
        // 在sl->_arr位置增容空间,如果空间不够就划出一个新的空间,然后将生成的空间返回给tmp

        if (tmp  NULL)
        {
            printf("memory realloc failed!\n");
            return;
        }
        sl->_arr = tmp; // 获取指向的数组(因为sl->arr原位置可能空间不足，划出了新的空间)
        sl->_capacity = newcapacity;
    }
}

#pragma region 增删查改
// 尾插
void SeqListPushBack(SL* sl, SLDataType x)
{
    SeqListCheckCapacity(sl);

    sl->_arr[sl->_size] = x;
    ++sl->_size;
}

// 头插(低效)
void SeqListPushFront(SL* sl, SLDataType x)
{
    SeqListCheckCapacity(sl);

    // 找尾巴,挪空间
    int end = sl->_size - 1;
    while (end >= 0)
    {
        sl->_arr[end + 1] = sl->_arr[end];
        --end;
    }
    sl->_arr[0] = x;
    ++sl->_size;
}

// 尾删
void SeqListPopBack(SL* sl)
{
    if (sl->_size  0)
    {
        printf("Don't have any statistic!\n");
        return;
    }

    --sl->_size;
}

// 头删(低效)
void SeqListPopFront(SL* sl)
{
    if (sl->_size  0)
    {
        printf("Don't have any statistic!\n");
        return;
    }

    // 挪空间
    int begin = 0;
    while (begin < sl->_size - 1)
    {
        sl->_arr = sl->_arr[begin + 1]; // 两边的语句是同时执行的,写++begin是没有用的
        ++begin;
    }
    --sl->_size;
}

// 查找
size_t SeqListFind(SL* sl, SLDataType x)
{
    size_t begin = 0;
    while (begin < sl->_size)
    {
        if(sl->_arr  x)
        {
            return begin;
        }
        ++begin;
    }
    return -1; // 返回无符号类型的最大值,表示没有找到
}

// 插入
void SeqListInsert(SL* sl, size_t pos, SLDataType x)
{
    if (pos > sl->_size) // 如果索引值不合法
    {
        printf("illeagel index\n");
        return;
    }

    SeqListCheckCapacity(sl);

    int end = sl->_size - 1;
    while (end >= pos)
    {
        sl->_arr[end + 1] = sl->_arr[end];
        --end;
    }
    sl->_arr[pos] = x;
    ++sl->_size;
}

// 擦除
void SeqListErase(SL* sl, size_t pos)
{
    if (pos >= sl->_size) // 如果索引值不合法
    {
        printf("illeagel index\n");
        return;
    }

    int begin = pos;
    while (begin < sl->_size - 1)
    {
        sl->_arr = sl->_arr[begin + 1];
        ++begin;
    }
    --sl->_size;
}
#pragma endregion

• 测试结果

  • 结果1：头插，尾插和头删，尾删

  

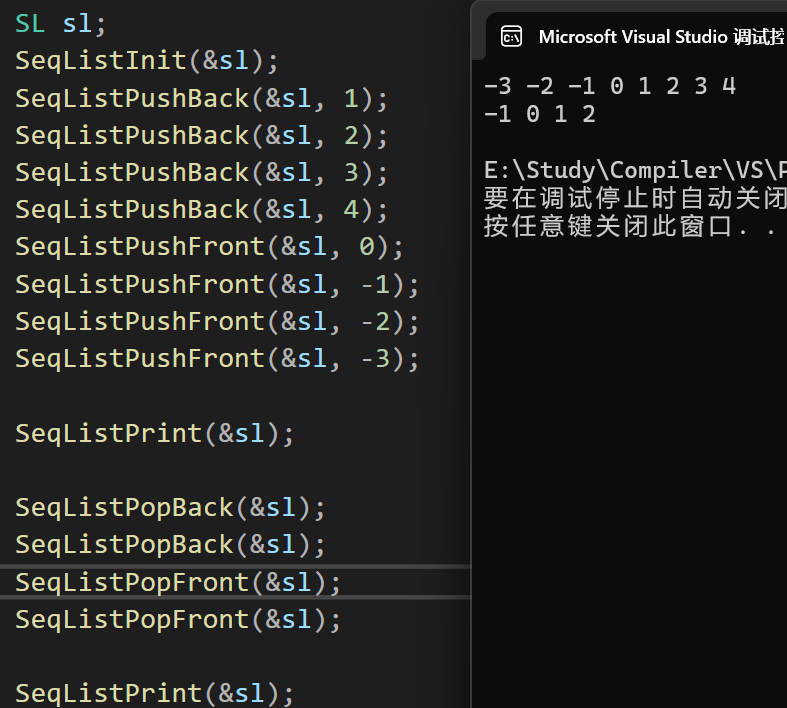
  • 结果2：插入，删除和查找

  

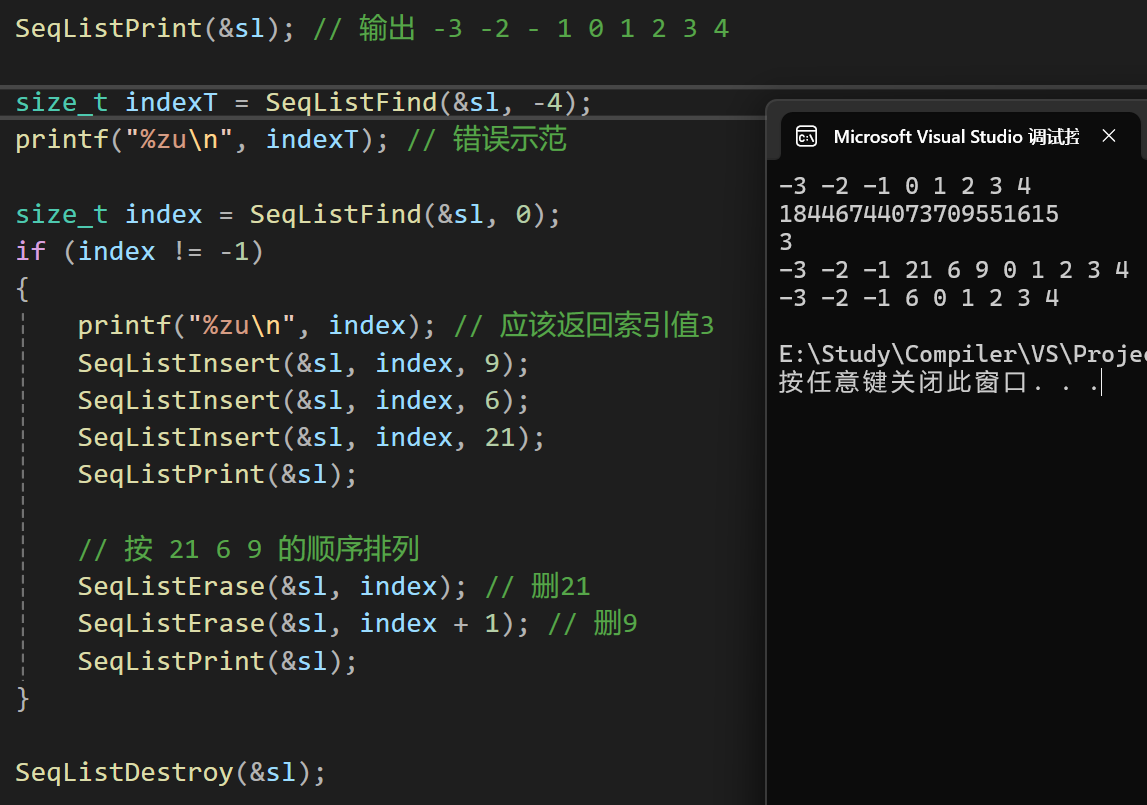
总结：优点与缺点💡

• 优点：
  1. 支持随机访问,需要数据访问结构支持的算法(如二分法和排序算法)能很好的适用
  2. Cpu高速缓存(也称Cache)的命中率更高，因为顺序表在内存中是连续储存的，它在遍历时能够更好的利用Cpu高速缓存 (这是相对于链表而言的)。其详细的原因如下：
     • 局部性原理(Locality Principle)：对于计算机相系统而言，如果某个数据被访问过，那么很可能在短时间内再次被访问，而且它附近的数据很可能也会被访问，而顺序表中元素是连续存储的，所以CPU预取机制可以提前将下一批数据加载到缓存中，避免频繁访问主存(也称RAM)
     • CPU预取机制(Prefetch)：顺序表中元素是连续存储的，CPU 可以预测下一个要访问的数据地址并提前加载到缓存中
     • 减少缓存不命中(Cache Miss)：顺序表的元素紧密排列，访问相邻元素时更容易命中缓存
• 缺点：
  1. 头部中部插入删除时间效率低O(N)
  2. 因为顺序表时连续的物理空间，如果空间不够了会增容，增容有一定程度的时间和空间消耗，尤其是增容拷贝时的消耗会很大
  3. 增容的空间可能用不完，这会造成空间的浪费

1.2：链表🔗

• 起源：前面我们谈到了顺序表对头部的操作效率很低，而且增容可能会浪费很多的空间，并且在内存碎片化的环境下，顺序表的增容会变得很困难，这些缺点都很致命，尤其是在上世纪电脑容量很小的情况下，而为了解决顺序表在一定应用场景下的不足，链表就被创造了出来，链表通过节点间的指针链接解决了这些问题
• 实质：链表的实质是一个由节点组成的线性数据结构，每个节点都包含存储的数据和指向下一个节点的指针 (不同的链表也可能有指向前一个节点的指针)

分类

• 链表具体可以分为三种基本类型：

  • 单向链表(Singly Linked List)：每个节点只有一个指向下一个节点的指针，尾节点的指向下一个节点的指针指向NULL
  • 双向链表(Doubly Linked List)：每个节点有两个指针，一个指向下一个节点，另一个指向前一个节点，头节点的指向上一个节点的指针指向NULL，尾节点的指向下一个节点的指针指向NULL
  • 循环链表(Circular Linked List)：单向链表或双向链表的变种，其中最后一个节点的指针指向头节点，而不是 NULL

• 这三种基础类型再加上哨兵位头节点可以组合出多种不同的链表，我们主要讨论最复杂和最简单的两个链表

  1. 单链表(不带头)：单链表是最简单实现的链表

     • 它的头尾部插入和删除的效率都很高，为O(1)，但是位于中间位置的插入和删除的效率很低，需要遍历链表，为O(N)
     • 只能进行单向遍历，从头节点开始顺序访问
     • 单链表在进行删除等操作时，需要处理特殊情况以避免报错

  2. 带头双向循环链表：带头双向循环链表是最复杂实现的链表

     • 由于有两个指针，在任意处的插入和删除的效率都很高，为O(1)
     • 支持双向遍历，可以从任意位置开始向前或向后遍历，在某些特殊应用场景(如频繁的双向遍历)下能提高效率
     • 由于是循环链表，带头双向循环链表进行任何操作时几乎都不需要进行特殊处理，方便了程序员编写代码

     特性	单链表	双向链表
     内存占用	1指针	2指针
     逆向遍历	❌	✅

• ⚠️在下文中，我们讨论带头双向循环链表，暂时先不讨论单链表

核心

#pragma once
#include <stdio.h>
#include <stdlib.h>
// 定义数据类型别名，方便修改数据类型
typedef int DLDataType;

typedef struct DListNode
{
    // 带头双向循环链表的成员：数据，前指针，后指针
    DLDataType _data;
    struct DListNode* _next;
    struct DListNode* _prev;
} DLNode;

// 以下为需要实现的函数的声明
void DListPrint(DLNode* pHead);

// 构造与析构
DLNode* DListInit(); // TODO：返回头指针
void DListDestroy(DLNode** ppHead); // TODO：要改变头指针指向的地址，所以要传二级指针

// 增删查改(带头不用二级指针)
void DListPushBack(DLNode* pHead, DLDataType data);
void DListPushFront(DLNode* pHead, DLDataType data);
void DListPopBack(DLNode* pHead);
void DListPopFront(DLNode* pHead);
DLNode* DListFind(DLNode* pHead, DLDataType data);
void DListInsert(DLNode* pHead, DLNode* pos, DLDataType data);
void DListErase(DLNode* pHead, DLNode* pos);

接口⚙️

构造与析构

• 初始化：
  • DListInit：用于初始化链表的结构，创建一个哨兵头节点(该节点不储存数值)，并使这个带头双向循环链表形成一个双向循环的结构，最后返回该节点的拷贝，需要人为手动初始化才是一个能够使用的链表
• 销毁：
  • DListDestroy：当带头双向循环链表不需要使用时，就需要手动销毁这个链表，以防内存泄漏，注意是一定要传入哨兵头节点的指针的地址

#pragma region 构造与析构
// 初始化
DLNode* DListInit()
{
    DLNode* SentryHead = BuyNode(0); // 为了方便统一管理，头结点的数据放0
    SentryHead->_next = SentryHead;
    SentryHead->_prev = SentryHead;

    return SentryHead;
}

// 销毁
void DListDestroy(DLNode** ppHead)
{
    if (*ppHead  NULL || ppHead  NULL)
    {
        printf("invalid pointer!\n");
        exit(-10);
    }

    DLNode* cur = (*ppHead)->_next;
    // DLNode* next = cur->_next; // TODO:这样在cur被释放后在更新是会导致Use-After-Free 

    while (cur != *ppHead)
    {
        DLNode* next = cur->_next; // 在cur释放前获取它的后一个指针
        free(cur);
        cur = next;
    }

    free(*ppHead);
    *ppHead = NULL;
}
#pragma endregion

• 解释一下什么是Use-After-Free ：free(cur)的作用只是让开发者不能再次访问已释放的空间(已被系统回收)，不会将指针置空，cur和next仍然指向原来储存的地址值，此时cur和next变成了悬空指针，指向已释放的内存，此时若访问(解引用)悬空针指,就会导致Use-After-Free,导致崩溃,但是直接赋值是不会报错的,因为它只是拷贝地址值,而不会解引用地址

• 测试结果：

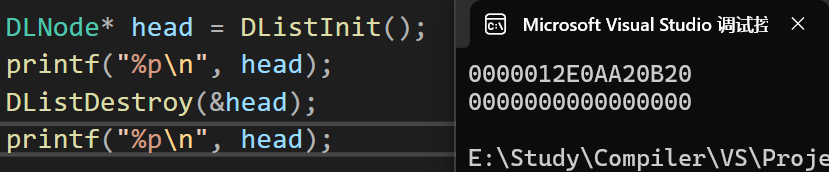
增删查改✂️

• 带头双向链表操作

操作	函数	时间复杂度	说明
✅ 增	DListPushBack	O(1)	在头节点前驱插入（等效尾插）
	DListPushFront	O(1)	在头节点后继插入（等效头插）
❌ 删	DListPopBack	O(1)	删除头节点前驱节点（等效尾删）
	DListPopFront	O(1)	删除头节点后继节点（等效头删）
🔍 查	DListFind	O(n)	从首节点开始线性搜索节点
✏️ 改	DListInsert	O(1)	在已知pos节点处插入（需前置查找）
	DListErase	O(1)	删除已知pos节点（需前置查找）

// 将其设为静态可以防止其他模块误用或依赖这个实现细节
static DLNode* BuyNode(DLDataType data)
{
    DLNode* tmp = (DLNode*)malloc(sizeof(DLNode));
    if (tmp  NULL)
    {
        printf("memory allocation failed!\n");
        return;
    }
    tmp->_data = data;

    return tmp;
}

void DListPrint(DLNode* pHead)
{
    DLNode* cur = pHead->_next;
    while (cur != pHead)
    {
        printf("%d ", cur->_data);
        cur = cur->_next;
    }
    printf("\n");
}

#pragma region 增删查改
// 尾插:在哨兵头节点的上一个位置插入数据
void DListPushBack(DLNode* pHead, DLDataType data)
{
    DLNode* newNode = BuyNode(data);

    DLNode* tail = pHead->_prev;
    newNode->_prev = tail;
    newNode->_next = pHead;
    pHead->_prev = newNode;
    tail->_next = newNode;
}

// 头插:在哨兵头节点的下一个位置插入数据
void DListPushFront(DLNode* pHead, DLDataType data)
{
    DLNode* newNode = BuyNode(data);

    DLNode* next = pHead->_next;
    newNode->_next = next;
    newNode->_prev = pHead;
    pHead->_next = newNode;
    next->_prev = newNode;
}

// 尾删:删掉哨兵头节点的前一位数据
void DListPopBack(DLNode* pHead)
{
    if (pHead->_next  pHead)
    {
        printf("This LinkedList is Empty!\n");
        return;
    }
    DLNode* prev = pHead->_prev;

    prev->_prev->_next = pHead;
    pHead->_prev = prev->_prev;
    free(prev);
    prev = NULL; // 置空,防止使用悬空指针
}

// 头删:删掉哨兵头节点的下一位数据
void DListPopFront(DLNode* pHead)
{
    if (pHead->_next  pHead)
    {
        printf("This LinkedList is Empty!\n");
        return;
    }
    DLNode* next = pHead->_next;

    next->_next->_prev = pHead;
    pHead->_next = next->_next;
    free(next);
    next = NULL; 
}

// 查找:从头开始查出第一个数据为data大小的节点
DLNode* DListFind(DLNode* pHead, DLDataType data)
{
    if (pHead->_next  pHead)
    {
        printf("This LinkedList is Empty!\n");
        return;
    }
    DLNode* cur = pHead->_next;

    while (cur != pHead)
    {
        if (cur->_data  data)
        {
            return cur;
        }
        cur = cur->_next;
    }

    return NULL; // 没找到返回空指针
}

// 插入:在指定位置插入数据
void DListInsert(DLNode* pHead, DLNode* pos, DLDataType data)
{
    DLNode* newNode = BuyNode(data);
    DLNode* posPrev = pos->_prev;

    posPrev->_next = newNode;
    pos->_prev = newNode;
    newNode->_next = pos;
    newNode->_prev = posPrev;
}

// 删除:在指定的位置删除数据
void DListErase(DLNode* pHead, DLNode* pos)
{
    if (pHead->_next  pHead)
    {
        printf("This LinkedList is Empty!\n");
        return;
    }
    // 防止删除头节点
    if (pos  pHead)
    {
        pos = pos->_next;
    }
    pos->_prev->_next = pos->_next;
    pos->_next->_prev = pos->_prev;
    free(pos);
    pos = NULL;
}
#pragma endregion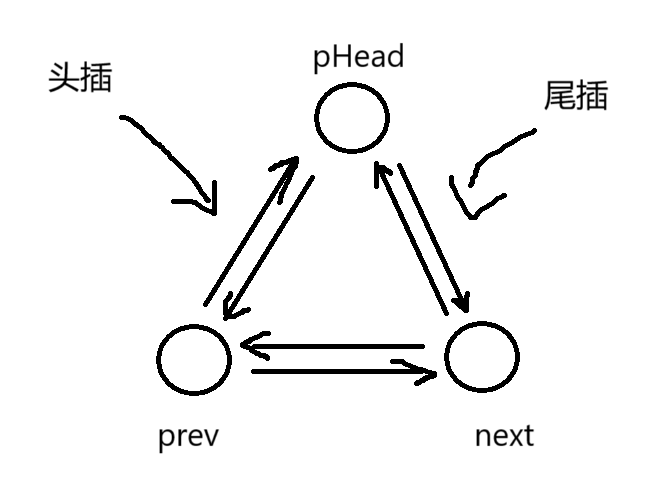

• 测试结果

  • 结果1：头插，尾插和头删，尾删

  

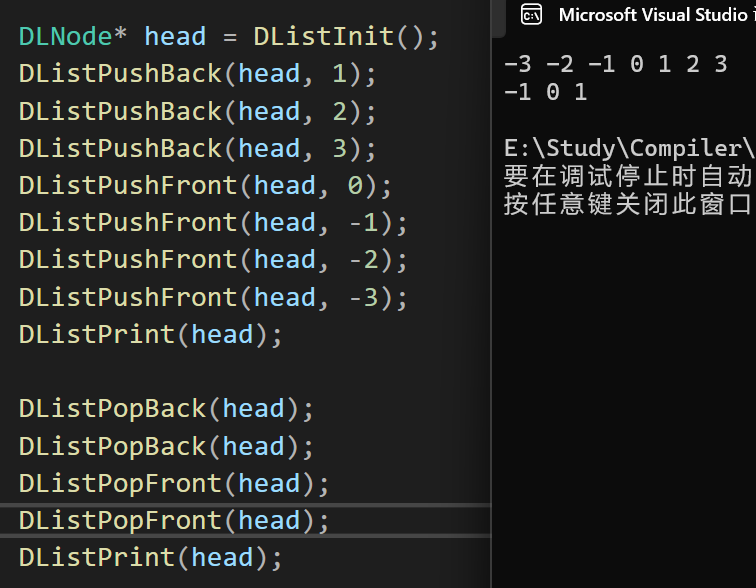
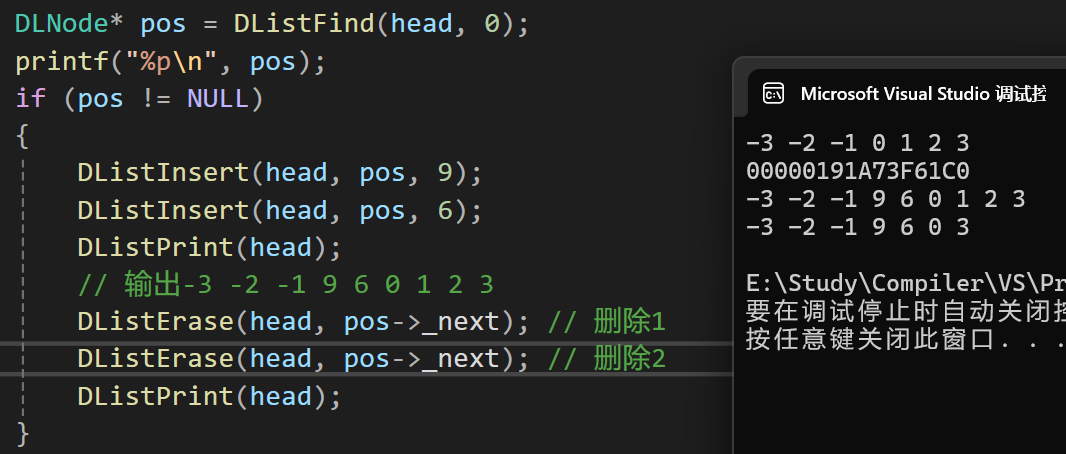
  • 结果2：插入，删除和查找

  

总结：优点与缺点💡

• 优点：
  1. 任意位置插入删除的效率都很高(为O(1))
  2. 可以按需申请和释放空间，不会造成空间的浪费
  3. 能构成高级结构基础(如哈希桶，图的邻接表等等)
• 缺点：
  1. 不支持随机访问(索引访问)，意味着一些算法是不适用的(如排序算法，二分查找算法等等)
  2. 链表储存一个值，同时要储存链接指针，也有一定的消耗 [单链表1个指针，双向链表2个指针]
  3. cpu高速缓存命中率更低(节点内存不连续，无法预加载)

顺序表VS链表

应用场景	顺序表优势 📊	链表优势 🔗
🎯频繁随机访问	✓
🔄频繁头尾插入/删除		✓
💾内存受限环境		✓
🚀缓存友好	✓
📈数据规模变化剧烈		✓

1.3：栈🗂️

• 概念：栈是一种模拟计算机栈结构的数据结构，栈是一种特殊的线性表，具有LIFO(Last in First out)的结构特点，栈有特殊的结构，用户只能在栈的其中一段插入(压栈)或删除(弹栈)数据，插入或进行删除操作的一段称为栈顶，另一端则称为栈底

  // 示范：
  栈顶 Top
    ↑
  +-------+
  |   8   |  ←  最新压入的元素
  +-------+
  |   5   |
  +-------+
  |   2   |  ←  最早压入的元素（栈底）
  +-------+

数据栈VS系统栈

• 谈到栈，就不得不比较一下系统栈(硬件层面)和数据栈(数据结构层面)间相同点和不同点了

不同点

对比维度	数据结构栈	计算机系统栈
本质	抽象的数据结构（逻辑模型）	内存中的物理存储区域（物理模型）
实现方式⚙️	可用数组/链表自由实现	由CPU和操作系统强制管理的连续内存区域
操作权限	开发者完全控制（可自定义压栈/弹栈规则）	由系统自动管理（开发者无法直接干预）
存储内容📦	任意数据类型	函数调用信息（返回地址、局部变量等）
大小限制📏	取决于实现方式（可动态扩容）	固定大小（由系统预设，可能栈溢出）
生命周期⏱️	由程序显式创建和销毁	随线程/进程自动创建和释放

相同点

• 数据栈是模仿系统栈的逻辑结构而设计出的一种数据结构，所以他们也有很多的相同点

特性	说明
LIFO原则	两者都遵循后进先出（Last-In-First-Out）的规则
基本操作	都支持压栈（Push）和弹栈（Pop）操作
栈顶指针	均通过指针/寄存器（如ESP）跟踪当前栈顶位置
溢出风险	都可能因过度压栈导致栈溢出（链表栈可能耗尽内存 递归太深导致Stack Overflow）

分类

基于实现

• 顺序栈：

  • 实现：一般用动态顺序表模拟出栈的结构，顺序表的尾部即为栈顶
  • 特点：
    1. 需要动态扩容，可能存在空间浪费
    2. 插入删除很方便

• 链式栈：

  • 实现：使用无头单链表进行模拟，链表的头节点即为栈顶
  • 特点：
    1. 无容量限制，依据数据个数创建空间
    2. 插入操作需要处理指针

基于功能

• 普通栈：

  • 基本LIFO功能
  • 只支持push/pop/peek等基本操作

• 最小栈/最大栈：

  • 额外维护当前栈的最小值或最大值
  • 可以在O(1)时间内获取栈中的最小/最大值

• 双栈（共享栈）：

  • 两个栈共享同一存储空间
  • 一个栈从数组头部开始增长，另一个从尾部开始
  • 提高内存利用率
  • 常用于特定算法或内存受限环境

• 单调栈：

  • 栈内元素保持单调递增或递减的顺序
  • 用于解决特定算法问题（如寻找下一个更大元素）

• ⚠️在下文中，我们将用单链表实现一个链式栈

核心

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
typedef int STDataType;

// 数据节点及其关系设计
typedef struct StackNode
{
    int _data;
    struct StackNode* _next;
}STNode;

// 数据结构
typedef struct
{
    size_t _size; // 栈中元素个数
    STNode* _top; // 栈顶
}LinkedStack;

// 构造与析构
void StackInit(LinkedStack* stack);
void SackDestroy(LinkedStack* stack);

// 增删查
void Push(LinkedStack* stack, STDataType data);
void Pop(LinkedStack* stack);
STDataType Peek(LinkedStack* stack);

// 其他
bool IsEmpty(LinkedStack* stack);
size_t Size(LinkedStack* stack); // 由于C语言没有封装的概念,所以GetSize函数可写可不写

• LinkedStack的结构体功能：
  • 在函数中修改头节点的值时不再需要给函数传二级指针作为参数

接口⚙️

构造与析构

• 初始化：

  • StackInit：为新创建的链式栈的成员一个初始值，方便stack在其他函数中的使用

• 销毁：

  • StackDestroy：当栈不需要被使用时，调用此函数将栈销毁，防止内存泄漏

#pragma region 构造与析构
// 初始化
void StackInit(LinkedStack* stack)
{
    stack->_top = NULL; // 栈顶为空
    stack->_size = 0;
}

// 销毁
void StackDestroy(LinkedStack* stack)
{
    while (stack->_top != NULL)
    {
        STNode* cur = stack->_top;
        stack->_top = cur->_next; // 更新栈顶(最后一个空间的下一个位置为NULL)
        free(cur); // cur为悬空指针,但是cur是局部变量,所以不用置为NULL
    }
    stack->_size = 0;
}
#pragma endregion

增删查✂️

操作	函数	时间复杂度	说明
✅ 增	Push	O(1)	向栈顶位置添加数据
❌ 删	Pop	O(1)	获取并移除栈顶的数据
🔍 查	Peek	O(1)	获取栈顶的数据（不移除）
📏 查	Size	O(1)	获取当前栈中元素数量
◻️ 查	IsEmpty	O(1)	判断栈是否为空

static STNode* BuyNode(STDataType data)
{
    STNode* tmp = (STNode*)malloc(sizeof(STNode));

    if (tmp  NULL)
    {
        printf("realloc failed!\n");
        return;
    }
    tmp->_next = NULL; // 指向NULL
    tmp->_data = data;

    return tmp;
}

#pragma region 增删查
// 压栈
void Push(LinkedStack* stack, STDataType data)
{
    STNode* newNode = BuyNode(data);
    newNode->_next = stack->_top; 
    stack->_top = newNode; // newNode就是新的栈顶,所以其他数据应该接在newNode后面
    ++stack->_size;
}

// 弹栈
STDataType Pop(LinkedStack* stack)
{
    if (stack->_top  NULL)
    {
        printf("Empty Stack!\n");
        return; 
    }

    STNode* tmp = stack->_top;
    stack->_top = tmp->_next;
    free(tmp);
    tmp = NULL;
    --stack->_size;

    return stack->_top->_data;
}

// 获取栈顶
STDataType Peek(LinkedStack* stack)
{
    if (stack->_top  NULL)
    {
        printf("Empty Stack!\n");
        return; 
    }

    return stack->_top->_data;
}

// 是否为空
bool IsEmpty(LinkedStack* stack)
{
    return stack->_top  NULL;
}

// 获取数据个数
size_t Size(LinkedStack* stack)
{
    return stack->_size;
}
#pragma endregion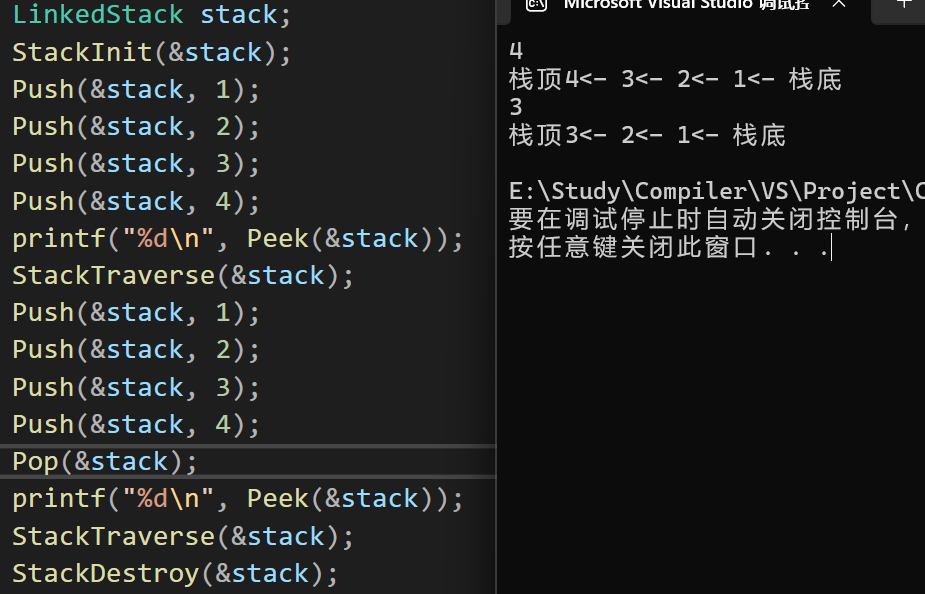

总结：优势及适用场景💡

• 优势：

  1. 低内存开销：只需要维护栈顶指针，不需要额外存储结构
  2. 逻辑清晰：LIFO特性使某些问题的解决变得直观
  3. 递归替代：可以用栈替代递归实现，避免递归深度限制
  4. 临时存储：适合需要"最近使用"或"后进先出"的场景

• 应用场景：

  1. 括号匹配检查：
     • 检查代码中的括号是否正确嵌套
     • 遇到左括号压栈，遇到右括号弹出并匹配
  2. 回溯算法：
     • 深度优先搜索（DFS）的非递归实现
     • 迷宫求解等路径探索问题
  3. 撤销（Undo）功能：
     • 文本编辑器中的撤销操作通常使用栈实现
     • 每次操作压栈，撤销时弹出

1.4：队列📥

• 概念：队列是一种特殊的线性表，具有FIFO(First in First out)的结构特点，队列有特殊的结构，用户只能再队列的一段进行插入(入队)，并且在另一端删除(出队)，插入数据的一端称为队尾，删除数据的一端称为对头
• 实现：实现队列能用链表，只有链式队列才能高效使用(要实现高效的头插和尾插)

分类

• 普通队列（FIFO Queue）

  • 标准队列，严格遵循 先进先出（FIFO）

  • 操作：enqueue()（入队）、dequeue()（出队）、peek()（查看队首）

• 双端队列（Deque, Double-Ended Queue）

  • 允许 两端（队首和队尾） 进行插入和删除

  • 变种：

  • 输入受限 Deque：只能一端入队，两端出队

  • 输出受限 Deque：只能一端出队，两端入队

• 优先队列（Priority Queue）

  • 元素按 优先级 出队（而非FIFO，或者说是通过优先级排出的队列）

  • 实现方式：堆（Heap）、有序数组/链表

• 循环队列（Circular Queue）

  • 底层是数组，但 rear/back 和 front 可以循环移动，避免空间浪费

• 阻塞队列（Blocking Queue）

  • 当队列 空时，出队操作阻塞；满时，入队操作阻塞

• 并发队列（Concurrent Queue）

  • 线程安全，支持多线程环境下的高效入队/出队

  • 实现方式：

  • 加锁队列（如 ReentrantLock）

  • 无锁队列（如 CAS 原子操作）

• ⚠️在下文中，我们将用单链表实现一个链式队列

核心

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
typedef int QDataType;

typedef struct QueueNode
{
    QDataType _data;
    struct QueueNode* _next;
}QNode;

// TODO:保存队列需要的对头和队尾两个接口,这样就不用使用二级指针了
typedef struct
{
    size_t _size;
    QNode* _head; // 队头:用于删除数据
    QNode* _tail; // 队尾:用于插入数据
}LinkedQueue;

// 构造与析构
void QueueInit(LinkedQueue* queue);
void QueueDestroy(LinkedQueue* queue);

// 增删查
void Push(LinkedQueue* queue);
void Pop(LinkedQueue* queue);

QDataType QueueBack(LinkedQueue* queue);
QDataType QueueFront(LinkedQueue* queue);
bool IsEmpty(LinkedQueue* queue);
size_t Size(LinkedQueue* queue);

接口⚙️

构造与析构

• 初始化：

  • QueueInit：为新创建的链式栈的成员一个初始值，方便stack在其他函数中的使用

• 销毁：

  • QueueDestroy：当栈不需要被使用时，调用此函数将栈销毁，防止内存泄漏

#pragma region 构造与析构
// 初始化
void QueueInit(LinkedQueue* queue)
{
    if (queue  NULL)
    {
        printf("illegal pointer!\n");
        return;
    }

    queue->_head = queue->_tail = NULL;
    queue->_size = 0;
}

void QueueDestroy(LinkedQueue* queue)
{
    if (queue  NULL)
    {
        printf("illegal pointer!\n");
        return;
    }

    // 从队头开始删除数据
    while (queue->_head != NULL)
    {
        QNode* cur = queue->_head; // 先写,避免野指针
        queue->_head = cur->_next;
        free(cur);
    }
    queue->_head = queue->_tail = NULL;
}
#pragma endregion

增删查✂️

操作	函数	时间复杂度	说明
✅ 入队	Push/enqueue	O(1)	入队，从队尾插入数据(尾插)
❌ 出队	Pop/dequeue	O(1)	出队，从队头删除数据(头删)
🔍 查	QueueFront	O(1)	获取队头数据
🔍 查	QueueBack	O(1)	获取队尾数据
◻️ 查	IsEmpty	O(1)	检查队列是否为空
📏 查	Size	O(1)	返回队列元素个数

• ⚠️tip：写代码一般遵循代码复用的原则，来减少程序员的代码量，下列实现核心代码时会有代码复用

static QNode* BuyNode(QDataType data)
{
    QNode* tmp = (QNode*)malloc(sizeof(QNode));

    if (tmp  NULL)
    {
        printf("memory allocation failed!\n");
        return;
    }

    tmp->_data = data;
    tmp->_next = NULL;

    return tmp;
}

#pragma region 增删查
// 入队(enqueue)
void Push(LinkedQueue* queue, QDataType data) 
{
    if (queue  NULL)
    {
        printf("illegal pointer!\n");
        return;
    }
    QNode* newNode = BuyNode(data);

    if (queue->_head  NULL) // 没有数据
    {
        queue->_head = queue->_tail = newNode;
    }
    else
    {
        queue->_tail->_next = newNode; // 尾插
        queue->_tail = newNode; // 更新尾节点位置
    }
    ++queue->_size;
}

// 出队(dequeue)
void Pop(LinkedQueue* queue)
{
    if (IsEmpty(queue))
    {
        printf("Empty Queue!\n");
        return;
    }

    QNode* oldHead = queue->_head; // 保存旧地址,减少重复访问
    queue->_head = oldHead->_next;
    free(oldHead);
    oldHead = NULL; // 防止意外访问野指针
    if (queue->_head  NULL)
    {
        queue->_tail = NULL; // 最后一个结点时,_tail指针也要置空
    }
    --queue->_size;
}

// 查看队尾
QDataType QueueBack(LinkedQueue* queue)
{
    // 先检查是否为空
    if (IsEmpty(queue))
    {
        printf("Empty Queue!\n");
        return;
    }

    return queue->_tail->_data;
}

// 查看对头
QDataType QueueFront(LinkedQueue* queue)
{
    // IsEmpty会检查queue是否空
    if (IsEmpty(queue))
    {
        printf("Empty Queue!\n");
        return;
    }

    return queue->_head->_data;
}

// 是否为空
bool IsEmpty(LinkedQueue* queue)
{
    if (queue  NULL)
    {
        printf("illegal pointer!\n");
        return;
    }
    return  queue->_head  NULL;
}

// 数据个数
size_t Size(LinkedQueue* queue)
{
    if (queue  NULL)
    {
        printf("illegal pointer!\n");
        return;
    }

    return queue->_size;
}
#pragma endregion

• 测试结果：

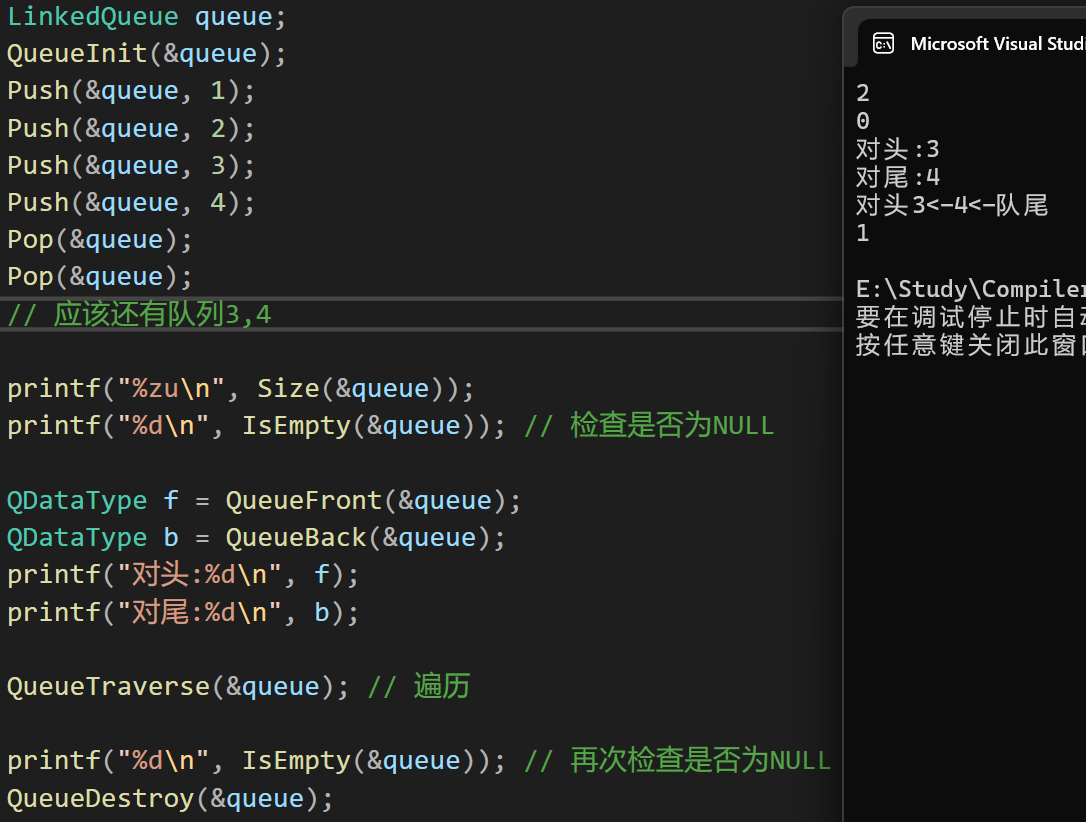
总结：优势及适用场景💡

• 优势：

  • 简单高效
  • 基于先进先出（FIFO）原则，逻辑简单，易于实现（如数组或链表）。
  • 入队（enqueue）和出队（dequeue）操作的时间复杂度通常为 O(1)（需避免数组实现的频繁扩容）。
  • 顺序性保障
  • 严格按任务到达的顺序处理，适合需要公平性的场景（如打印任务队列）。
  • 低内存开销
  • 普通队列只需维护头尾指针，占用空间少。

• 适用场景：

  • 任务调度
  • CPU 进程调度、打印机任务队列等需要按到达顺序处理的场景。
  • 广度优先搜索（BFS）
  • 按层级遍历树或图结构时，队列天然满足“先探索的节点先扩展”的需求。
  • 消息缓冲
  • 异步通信中暂存消息（如生产者-消费者模型），缓解瞬时流量压力。
  • 实时系统
  • 事件处理（如点击事件、键盘输入）按触发顺序响应。
  • 基础数据结构扩展
  • 作为其他队列变种（如循环队列、阻塞队列）的基础实现。

Part2：树形结构

2.1：二叉树🌴

树

• 在正式介绍二叉树前，我们先了解以下什么是树以及在树结构中的一些名词

• 概念：树是一种非线性的数据结构，它是由n个有限节点组成一个具有层次关系的集合，倒过来看树的结构形态就会像是一颗树

术语

• 节点(Node)：树的基本单位，包含数据项和指向其他节点的指针

• 根节点(Root)：没有父节点的节点，树的顶端节点

• 父节点(Parent，双亲节点)：有子节点的节点

• 子节点(Child，孩子节点)：一个节点的直接下级节点

• 叶子节点(Leaf，终端节点)：没有子节点的节点

• 兄弟节点(Sibling)：具有相同父节点的节点

• 节点的度(Degree)：一个节点拥有的子节点数目

• 树的度(Degree)：即一棵树中最大的节点的度

• 层次(Level)：根节点为第1层，其子节点为第2层，以此类推

• 高度/深度(Height/Depth)：树中节点的最大层次

• 祖先(ancestor)：根节点到该节点所经分支上的所有节点

• 森林(forest)：n颗互不相交的多棵树组成的集合

树与非树

• 树的特征：

  1. 子树是不相交的

  2. 除根节点外，每个节点有且仅有一个父节点

  3. 一颗N个节点的树有N-1条边(N-1条线)

二叉树

• 概念：每个节点最多有两个子节点的树结构，这两个子节点被称为左子节点(左子树)和右子节点(右子树)

• 性质：

  • 对于任何二叉树，设度为0的叶子节点有n~0~个，度为2的分支节点有n~2~个，则一定有n~0~ = n~2~ + 1

  • 推导：设n~0~,n~1~,n~2~分别代表度为0,1,2的节点的个数,节点与连接的线条数的关系是n = L + 1，而L = n~1~ + 2n~2~; 故 n~0~ + n~1~ + n~2~ = n~1~ + 2n~2~ + 1，即可得出结论

  • 第i层上最多有2^(i-1)^个节点

  • 深度为k的二叉树最多有2^k^ - 1个节点(此时为满二叉树)

⚠️上述的语法可能在博客中有问题，其中a^b^：a的b次方，n~0~：n下标0

特殊二叉树

1. 完全二叉树: 除最后一层外，其他层节点数都达到最大值，且最后一层节点都集中在左侧
2. 满二叉树: 每一层的节点数都达到最大值，是特殊的完全二叉树
3. 堆：是一种特殊的完全二叉树，满足堆序性，分为大根堆和小根堆
   • 大根堆：父节点的值 ≥ 子节点的值 (根节点是最大值)
   • 小根堆：父节点的值 ≤ 子节点的值 (根节点是最小值)
4. 二叉搜索树(BST): 左子树上所有节点的值小于根节点，右子树上所有节点的值大于根节点
5. 平衡二叉树(AVL树): 任意节点的左右子树高度差不超过1
6. 红黑树: 一种自平衡二叉搜索树

遍历方式

1. 前序遍历(Pre-order): 根 → 左 → 右
2. 中序遍历(In-order): 左 → 根 → 右 (对BST会得到有序序列)
3. 后序遍历(Post-order): 左 → 右 → 根
4. 层次遍历(Level-order): 按层次从上到下，从左到右

• 通过遍历可以得出二叉树结构的组合:
  1. 前序+中序
  2. 后序+中序
  3. 中序+后序可以只能确定左子叶节点，前序+后序只能确定根节点

存储结构

1. 顺序存储: 使用数组，适合完全二叉树
2. 链式存储: 使用节点结构，包含数据域和左右指针域，一般把链式结构以下两种
   • 二叉链：是最基础的二叉树存储方式，只有左右两个孩子指针，每个节点包含：数据域 + 左孩子指针 + 右孩子指针
   • 三叉链(类似于双向链表)：对比二叉链多一个父节点指针，每个节点包含：数据域 + 左孩子指针 + 右孩子指针 + 父节点指针

应用

• 文件系统目录结构

• 数据库索引(B树、B+树)

• 哈夫曼编码(用于数据压缩)

• 决策树(机器学习)

• 语法分析树(编译器设计)

• ⚠️在下文中，我们将用二叉链实现一个普通二叉树

核心

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
typedef int BTDataType;

// 二叉树节点
typedef struct BinaryTreeNode
{
    BTDataType _data;
    struct BinaryTreeNode* _left;  // 左子树
    struct BinaryTreeNode* _right; // 右子树
}BTNode;

// 二叉树
typedef struct
{
    BTNode* root; // 保存根节点
}BinaryTree;

// 构造与析构
void BinaryTreeInit(BinaryTree* tree);
void BinaryTreeDestroy(BinaryTree* tree);

// 增删查改
BTNode* Insert(BinaryTree* tree, BTDataType data, BTNode* parent, bool isLeft);
void EraseSubtree(BinaryTree* tree, BTNode* node);
bool IsEmpty(BinaryTree* tree);
BTNode* FindParent(BinaryTree* tree, BTNode* node);
size_t Height(BinaryTree* tree);
size_t Size(BinaryTree* tree);

// 遍历
void PrevOrder(BinaryTree* tree);
void InOrder(BinaryTree* tree);
void PostOrder(BinaryTree* tree);
void LevelOrder(BinaryTree* tree);

接口⚙️

构造与析构

• 初始化：
  • BinaryTreeInit：为二叉树对象赋予初始值，方便后续对对象进行操作
• 销毁：
  • BinaryTreeDestroy：利用下面出现的BinaryTreeDestroy接口实现二叉树对象的销毁，防止内存泄漏

#pragma region 构造与析构
// 初始化
void BinaryTreeInit(BinaryTree* tree)
{
    tree->_root = NULL;
    tree->_size = 0;
}

// 销毁
void BinaryTreeDestroy(BinaryTree* tree)
{
    if (tree  NULL) {
        printf("Tree pointer is NULL!\n");
        return NULL;
    }

    if (tree->_root != NULL)
    {
        EraseSubtree(tree, tree->_root);
    }
}
#pragma endregion

增删查✂️

操作	函数	时间复杂度	说明
➕ 增	Insert	O(1)	向指定父节点的左/右子树插入数据，若父节点为空则作为根节点插入
✂️ 删	EraseSubtree	O(n)	删除从指定节点开始的整个子树（n为子树节点数）
🔍 查	FindParent	O(n)	查找指定节点的父节点（需遍历树）
◻️ 查	IsEmpty	O(1)	检查树是否为空（仅需判断根节点）
📏 查	Height	O(n)	计算树的高度（需遍历所有节点）
📊 查	Size	O(n)	统计树的节点总数（需遍历所有节点）
🍃 查	LeafSize	O(n)	计算叶子节点数量（需遍历所有节点）

static BTNode* BuyNode(BTDataType data)
{
    BTNode* tmp = (BTNode*)malloc(sizeof(BTNode));

    if (tmp  NULL)
    {
        printf("memory allocation failed!\n");
        return;
    }

    tmp->_data = data;
    tmp->_left = NULL; 
    tmp->_right = NULL; // 左右子树为NULL

    return tmp;
}

#pragma region 递归接口
// 删除这颗树
static void EraseSubtree_Recursive(BTNode* node)
{
    if (node  NULL)
    {
        return;
    }
    EraseSubtree_Recursive(node->_left);
    EraseSubtree_Recursive(node->_right);
    free(node);
}

static BTNode* FindParent_Recursive(BTNode* current, BTNode* target)
{
    if (current  NULL)
    {
        return NULL;
    }

    if (current->_left  target || current->_right  target)
    {
        return current;
    }

    BTNode* find = FindParent_Recursive(current->_left, target);
    if (find != NULL)
    {
        return find; // 返回NULL或current
    }
    // 返回NULL或current
    return FindParent_Recursive(current->_right, target);
}

static size_t Height_Recursive(BTNode* node)
{
    // node为NULL返回0,否则值+1;
    if (node  NULL)
    {
        return 0;
    }

    size_t leftHeight = Height_Recursive(node->_left);
    size_t rightHeight = Height_Recursive(node->_right);

    return (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;
}

static size_t Size_Recursive(BTNode* node)
{
    if (node  NULL)
    {
        return 0;
    }

    return Size_Recursive(node->_left) + Size_Recursive(node->_right) + 1;
}

static size_t LeafSize_Recursive(BTNode* node)
{
    // 1.自身为NULL
    if (node  NULL)
    {
        return 0;
    }
    // 2.没有子树
    if (node->_left  NULL && node->_right  NULL)
    {
        return 1;
    }
    // 3.有子树
    return LeafSize_Recursive(node->_left) + LeafSize_Recursive(node->_right);
}
#pragma endregion

#pragma region 增删查改
/// <summary>
/// 插入
/// </summary>
/// <param name="tree">:指向二叉树的指针，代表整棵树</param>
/// <param name="data">:要插入的新节点的数据</param>
/// <param name="parent">:要插入节点的父节点，如果为 NULL，则表示插入根节点</param>
/// <param name="isLeft">:指示是否将新节点插入到 parent 的左子节点</param>
/// <returns></returns>
BTNode* Insert(BinaryTree* tree, BTDataType data, BTNode* parent, bool isLeft)
{
    if (tree  NULL) {
        printf("Tree pointer is NULL!\n");
        return NULL;
    }

    // 先创建一个节点
    BTNode* newNode = BuyNode(data);

    // 1.插入根节点(不存在父节点)
    if (parent == NULL){
        if (tree->_root != NULL){
            printf("node have existed!\n");
            free(newNode);
            newNode = NULL;
            return NULL;
        }
        tree->_root = newNode;
        ++tree->_size;
        return newNode;
    }

    // 2.插入左子树或右子树(存在父节点)
    BTNode** target = isLeft ? &(parent->_left) : &(parent->_right);
    // TODO:深拷贝一级指针要二级指针才能实现，解引用则没有这样的要求(TODO:即使浅拷贝,指向的空间也是相同的)
    if (*target != NULL) {
        printf("Target position is already occupied!\n");
        free(newNode);
        newNode = NULL;
        return NULL;
    }

    ++tree->_size;
    *target = newNode;
    return newNode;
}

/// <summary>
/// 删除子树
/// </summary>
/// <param name="tree">:指向二叉树的指针</param>
/// <param name="node">:删除从这个节点开始的整个子树</param>
void EraseSubtree(BinaryTree* tree, BTNode* node)
{
    if (tree  NULL || node  NULL) 
    {
        return; 
    }

    // 1.node为根节点(要删掉所有结点)
    if (node  tree->_root)
    {
        EraseSubtree_Recursive(node);
        tree->_root = NULL; // 置空,防止指向悬空指针
        return;
    }
    // 2.node不为根节点
    // 找到node的父节点,改变父节点的指向
    BTNode* parent = FindParent(tree, node);
    if (parent != NULL){
        if (node  parent->_left){
            parent->_left = NULL;
        }
        else{
            parent->_right = NULL;
        }
    }
    EraseSubtree_Recursive(node);
}

// 找节点的父节点
BTNode* FindParent(BinaryTree* tree, BTNode* node)
{
    if (tree->_root  node)
    {
        return NULL; // 无父节点
    }

    return FindParent_Recursive(tree->_root, node);
}

// 是否为空
bool IsEmpty(BinaryTree* tree)
{
    return tree->_root  NULL;
}

// 树的高度
size_t Height(BinaryTree* tree)
{
    if (tree  NULL)
    {
        printf("Tree pointer is NULL!\n");
        return;
    }
    return Height_Recursive(tree->_root);
}

// 节点个数
size_t Size(BinaryTree* tree)
{
    if (tree  NULL)
    {
        printf("Tree pointer is NULL!\n");
        return;
    }
    return Size_Recursive(tree->_root);
}

size_t LeafSize(BinaryTree* tree)
{
    if (tree  NULL)
    {
        printf("Tree pointer is NULL!\n");
        return;
    }
    return LeafSize_Recursive(tree->_root);
}
#pragma endregion

• 测试结果：

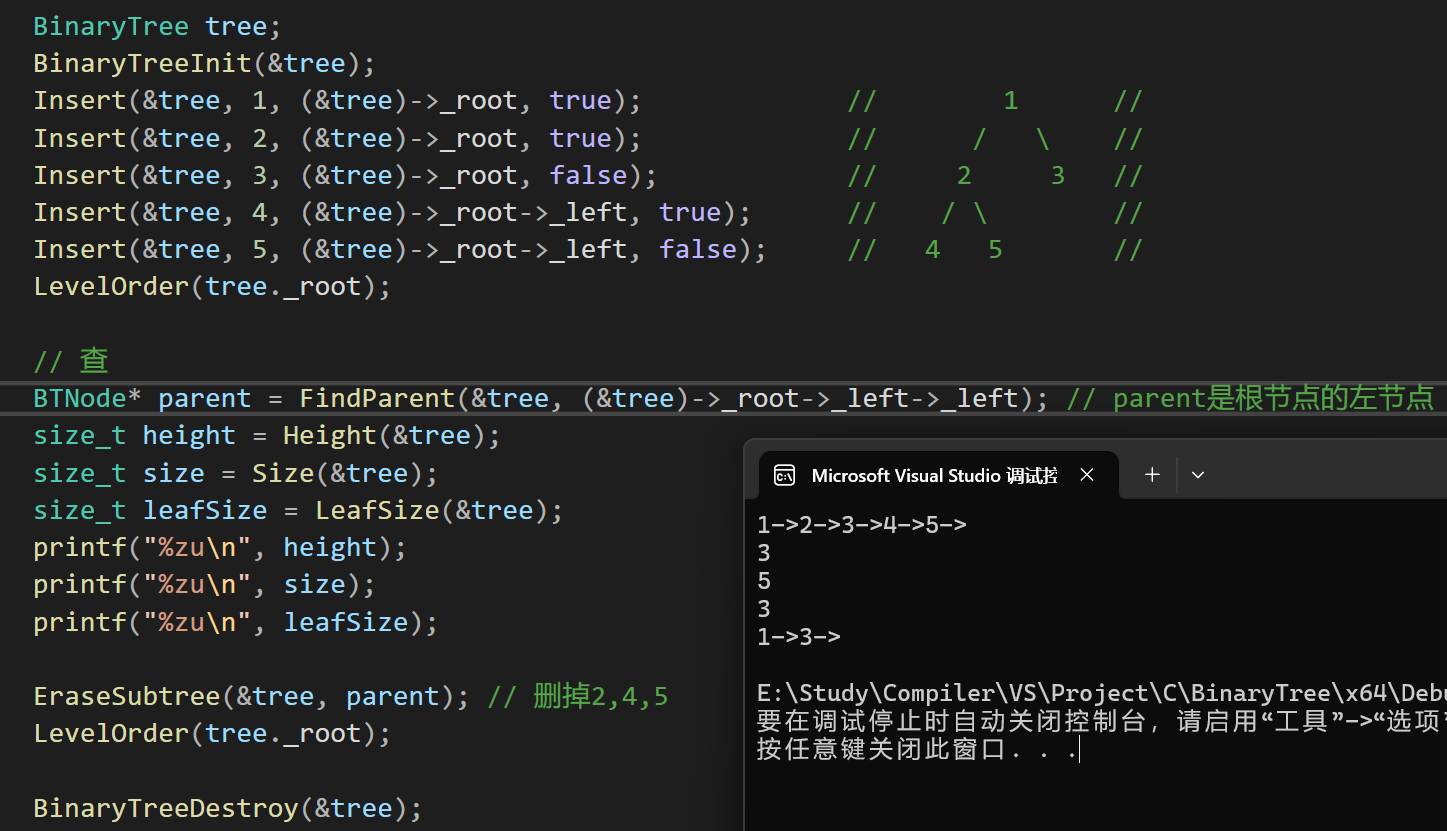
• 分治思想：上述递归算法(如计算节点个数和计算叶子节点个数)用到了分治思想，所以我现在要介绍一下什么是分治思想

• 步骤：

  1. 分解（Divide）：
     • 将原问题分解为若干个规模较小的子问题
     • 子问题应与原问题形式相同，只是规模更小
  2. 解决（Conquer）：
     • 递归地解决各个子问题
     • 当子问题足够小时，直接求解
  3. 合并（Combine）：
     • 将子问题的解合并为原问题的解

• 特征：

  • 问题可分解：问题可以分解为若干个相同形式的子问题
  • 子问题独立：各子问题之间没有重叠
  • 有终止条件：存在简单到可以直接求解的基本情况
  • 解可合并：子问题的解能够合并为原问题的解

遍历

• 树的遍历分四种，分别是前序，中序，后序和层序遍历
  • 前序（PrevOrder--深度优先遍历）：将节点中的数据按根节点->左节点->右节点的顺序递归遍历
  • 中序（InOrder--深度优先遍历）：将节点中的数据按左节点->根节点->右节点的顺序递归遍历
  • 后序（PostOrder--深度优先遍历）：将节点中的数据按左节点->右节点->根节点的顺序递归遍历
  • 层序(LevelOrder--广度优先遍历)：将节点中的数据逐层地，每层从左至右地进行遍历

#pragma region 遍历
// 前序遍历
void PrevOrder(BTNode* root)
{
    if (root  NULL)
    {
        printf("NULL "); // 打印NULL更好的体现结构
        return; // 遇见NULL开始返回
    }

    printf("%d->", root->_data); // 先打印根节点
    PrevOrder(root->_left);       // 再打印左节点
    PrevOrder(root->_right);  // 最后打印右节点
}

// 中序遍历
void InOrder(BTNode* root)
{
    if (root  NULL)
    {
        printf("NULL ");
        return;
    }

    InOrder(root->_left);         // 先打印左节点
    printf("%d->", root->_data); // 再打印根节点
    InOrder(root->_right);    // 最后打印右节点
}

// 后序遍历
void PostOrder(BTNode* root)
{
    if (root  NULL)
    {
        printf("NULL ");
        return;
    }

    PostOrder(root->_left);       // 先打印左节点
    PostOrder(root->_right);  // 再打印右节点
    printf("%d->", root->_data); // 最后打印根节点
}

// 层序遍历(广度优先遍历)
void LevelOrder(BTNode* root) // BFS
{
    LinkedQueue queue;
    QueueInit(&queue);
    if (root != NULL)
    {
        // root做为第一个遍历的节点,启动遍历
        Push(&queue, root);
    }
    while (!IsEmpty_Q(&queue))
    {
        BTNode* cur = QueueFront(&queue); 
        Pop(&queue);
        printf("%d->", cur->_data);

        // 从上至下,从左至右按顺序插入数据
        if (cur->_left != NULL)
        {
            Push(&queue, cur->_left);
        }
        if (cur->_right != NULL)
        {
            Push(&queue, cur->_right);
        }
    }
    printf("\n");
}
#pragma endregion

• 测试结果：

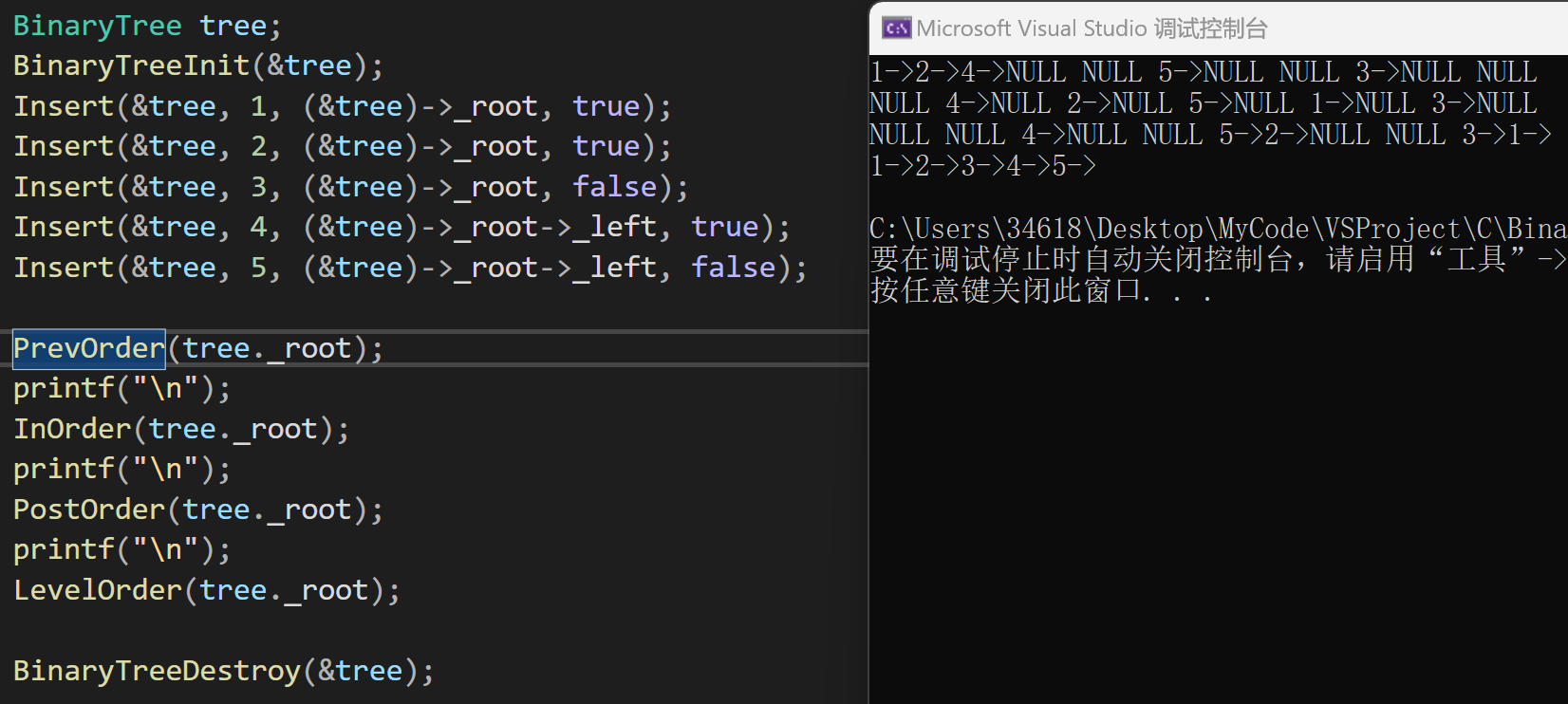
• 广度优先遍历(bfs)：上述层序遍历即是一个广度优先遍历，使用了之前数据结构——队列，广度优先遍历可以分成以下步骤

1. 初始化阶段：
   • 准备空队列，然后将起始根节点入队
2. 循环阶段：
   1. 取出当前节点，输出当前节点的数据
   2. 将当前节点的相邻未访问节点以一定的顺序(树是从左至右)入队

总结：二叉树的作用💡

• 二叉树的优势

优势	说明
层次表达能力	天然适合表示层级关系（如家谱、组织结构）
遍历方式多样	支持前/中/后序、层次遍历，适应不同处理逻辑
递归友好	天然的递归结构简化算法设计（如深度计算、子树操作）
扩展性强	可作为其他高级树结构（如AVL树、红黑树）的基础框架

• 应用场景

1. 层级数据表示

   • 文件系统目录结构

   • 公司组织架构图

   • 家谱/血缘关系树

• 优势：直观反映父子关系，便于可视化和管理

2. 表达式解析

   • 数学表达式树（如 (a+b)*c 的语法树）

   • 程序语法分析（编译器中的抽象语法树AST）

• 优势：中序遍历可还原表达式，前/后序遍历用于计算

3. 决策流程建模

   • 游戏AI的决策树

   • 业务流程审批树

• 优势：每个分支代表不同决策路径，逻辑清晰

4. 算法辅助结构

   • 堆排序中的完全二叉树

   • Huffman编码树（数据压缩）

   • 迷宫求解路径树

• 优势：临时构建辅助计算，任务完成后可释放

5. 网络数据路由

   • 网络包转发决策树

   • 聊天机器人对话流程树

• 优势：通过树节点跳转实现快速路由

2.2：堆📚

• 概念与特征：堆是一种特殊的完全二叉树数据结构，即除最后一层外，其他层节点都填满，最后一层从左到右填，而且堆要符合堆序性，即堆一定要是大堆(父节点的值 ≥ 子节点的值)或小堆(父节点的值 ≤ 子节点的值) [所以堆也被称为优先级队列]

堆维护

• 插入时："上浮"调整（Heapify Up）以维持堆性质
• 删除时："下沉"调整（Heapify Down）以维持堆性质

实现方式

• 堆通常使用数组来实现，因为数组刚好契合完全二叉树

• 对于在数组索引为i的节点，有以下关系：

  • 左子节点：2i + 1
  • 右子节点：2i + 2
  • 父节点：i为左子树：(i - 1) / 2 i为右子树：(i - 2) / 2,可以统一表示为floor((i-1)/2)(floor为向下取整函数)【完全二叉树的右子树的下标都是偶数，其实右子树用（i - 1）/ 2和（i - 2）/ 2的结果都是一样的】

• ⚠️在下文中，我们将用动态顺序表实现一个可变堆（大小堆可调）

核心

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
typedef int HpDataType;

typedef struct Heap
{
    HpDataType* _arr;
    size_t _size;
    size_t _capacity;
    bool _is_max_heap; // 标记是大根堆还是小根堆
}Heap;

void HeapPrint(Heap* heap);

// 构造与析构
void HeapInit(Heap* heap, bool isMaxHeap);
void HeapDestroy(Heap* heap);

// 增删查改
bool HeapCompare(Heap* heap, HpDataType a, HpDataType b);
void HeapPush(Heap* heap, HpDataType data);
void HeapPop(Heap* heap);
bool HeapTop(Heap* heap, HpDataType* value); // value为输出参数
void HeapShiftup(Heap* heap);
void HeapShiftdown(Heap* heap);

接口⚙️

构造与析构

• 初始化：
  • HeapInit：初始化堆的成员，方便后续函数的使用
• 销毁
  • HeapDestroy：销毁堆的成员，防止内存泄漏

#pragma region 构造与析构
void HeapInit(Heap* heap, bool isMaxHeap)
{
    heap->_arr = NULL;
    heap->_size = heap->_capacity = 0;
    heap->_is_max_heap = isMaxHeap;
}

void HeapDestroy(Heap* heap)
{
    if (heap != NULL)
    {
        free(heap->_arr);
        heap->_capacity = heap->_size = 0;
    }
}
#pragma endregion

调整函数

• 比较：
  • HeapCompare：通过判段heap是大根堆还是小根堆，来确定a(比较者)和b(被比较者)间的比较方式【类似于Cpp中的仿函数】
• 上浮：
  • HeapShiftup：在数据插入后（尾插），将新插入的元素与其父节点比较。若不满足堆序性，则交换两者，并继续向上调整，直到满足堆序性或达到堆顶。
• 下沉：
  • HeapShiftdown：在删除数据后（头删），将栈底元素移动至栈顶位置，然后将这个元素和它的较大子节点比较，若不满足堆序性，则交换两者，并继续向下调整，直到满足堆序性或该元素没有子节点

#pragma region 调整函数
// TODO:根据_is_max_heap来决定比较的符号,a为比较的数据,b是被比较者
bool HeapCompare(Heap* heap, HpDataType a, HpDataType b)
{
    return heap->_is_max_heap ? (a > b) : (a < b);
}

// 上浮(新元素插入堆底时，向上调整使其满足堆性质)
void HeapShiftup(Heap* heap)
{
    size_t index = heap->_size - 1;
    while (index > 0 && HeapCompare(heap, heap->_arr[index], heap->_arr[(index - 1) / 2]))
    {
        Swap(&heap->_arr[index], &heap->_arr[(index - 1) / 2]);
        index = (index - 1) / 2; // 上浮至父节点的位置
    }
}

// 下沉(堆顶元素被移除后，将最后一个元素移到堆顶并向下调整)
void HeapShiftdown(Heap* heap)
{
    size_t index = 0;
    size_t child = index * 2 + 1; // 默认是左孩子
    while (child < heap->_size) // 还有子节点
    {
        // 选出孩子中较大者或较小者(取决于对堆的类型)
        if (child + 1 < heap->_size && HeapCompare(heap, heap->_arr[child + 1], heap->_arr[child]))
        {
            ++child;
        }

        if (!HeapCompare(heap, heap->_arr[index], heap->_arr[child]))
        {
            Swap(&heap->_arr[index], &heap->_arr[child]);
            index = child;
            child = index * 2 + 1;
        }
        else
        {
            return; // index位置上的数据最大
        }
    }
}
#pragma endregion

增删查✂️

操作	函数	时间复杂度	说明
✅ 增	HeapPush	O(log n)	在堆底插入数据，并通过上浮调整维护堆序性
❌ 删	HeapPop	O(log n)	删除堆顶数据，将堆底元素移至堆顶，并通过下沉调整维护堆序性
🔍 查	HeapTop	O(1)	获取堆顶数据

// 交换
static void Swap(HpDataType* a, HpDataType* b)
{
    HpDataType tmp = *a;
    *a = *b;
    *b = tmp;
}

// 检查空间
static void CheckCapacity(Heap* heap)
{
    if (heap->_capacity  heap->_size)
    {
        size_t newCapacity = heap->_capacity  0 ? 4 : heap->_capacity * 2;
        HpDataType* tmp = (HpDataType*)realloc(heap->_arr ,sizeof(HpDataType) * newCapacity);
        if (!tmp)
        {
            printf("space realloc failed!\n");
            return;
        }

        heap->_arr = tmp;
        heap->_capacity = newCapacity;
    }
}

// 打印
void HeapPrint(Heap* heap)
{
    // 打印信息
    printf("Heap (%s): Size=%zu, Capacity=%zu\n",
        heap->_is_max_heap ? "Max" : "Min", heap->_size, heap->_capacity);
    printf("Elements: ");
    // 层序
    for (size_t i = 0; i < heap->_size; i++)
    {
        printf("%d ", heap->_arr[i]);
    }
    printf("\n");
}

#pragma region 增删查
// 插入数据并自动调整
void HeapPush(Heap* heap, HpDataType data)
{
    CheckCapacity(heap);

    heap->_arr[heap->_size] = data;
    ++heap->_size;
    HeapShiftup(heap);
}

// 删除数据并自动调整
void HeapPop(Heap* heap)
{
    if (heap->_size  0)
    {
        printf("no element exist!\n");
        return;
    }

    heap->_arr[0] = heap->_arr[heap->_size - 1]; // 将最后一个元素放到堆顶
    --heap->_size; // 尾删
    HeapShiftdown(heap);
}

// 获取栈顶数据
HpDataType HeapTop(Heap* heap)
{
    if (heap->_size  0)
    {
        printf("no element exist!\n");
        return;
    }

    return heap->_arr[0];
}
#pragma endregion

• 测试结果：

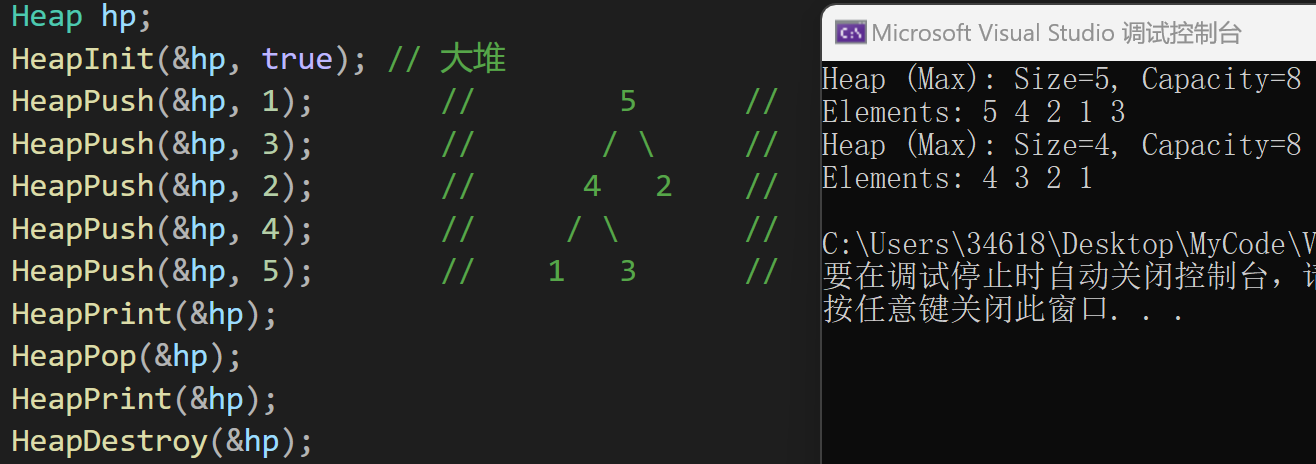
总结：堆的优势与应用💡

• 堆的优势

优势	说明
高效动态维护极值	大/小顶堆可在 O(1) 时间获取最大值/最小值，插入删除仅需 O(log n)
自动排序	插入数据后自动调整结构，始终维护堆序性（无需手动排序）
灵活可配置	通过调整比较逻辑，可快速切换大顶堆/小顶堆
支持动态扩容	可基于数组实现动态扩容（如2倍扩容策略）

• 堆的应用

1. 优先级队列（Priority Queue）

   • 场景：需要按优先级处理任务的场景（如CPU调度、急诊分诊）

   • 实现：大顶堆保证高优先级任务先出队

2. 堆排序（Heap Sort）

   • 步骤：

     1. 所有元素入堆（O(n log n)）
     2. 依次取出堆顶元素（O(n log n)）

   • 特点：原地排序，无需额外空间

3. Top K 问题

   • 求最大K个元素：维护容量为K的小顶堆，淘汰较小值

   • 求最小K个元素：维护容量为K的大顶堆，淘汰较大值

   • 时间复杂度：O(n log K)

4. 图算法优化

   • Dijkstra最短路径：用小顶堆快速选取未访问的最近节点

   • Prim最小生成树：用堆高效选择最小边

5. 事件驱动模拟

   • 场景：离散事件模拟（如银行排队系统）

   • 优势：按事件发生时间（小顶堆）自动排序处理

6. 多路归并

   • 场景：合并K个有序链表/数组

   • 实现：用堆维护K个指针的当前最小值

堆 VS 栈

• 既作为内存管理系统中的两个重要储存空间，还是两个常用的数据结构，所以有必要对比一下栈和堆的区别，以免弄乱定义

1. 数据结构层面

特性	堆（Heap）	栈（Stack）
数据结构类型	基于树的动态数据结构（完全二叉树）	线性数据结构（后进先出，LIFO）
存储方式	无序存储（但满足堆序性）	有序存储（按入栈顺序）
主要操作	插入（push）、删除极值（pop）	压栈（push）、弹栈（pop）
典型应用	优先级队列、排序、Top K问题	函数调用、表达式求值、回溯算法

• 访问方式

  特性	堆（Heap）	栈（Stack）
  访问权限	全局可访问（需指针）	仅当前函数或块作用域内访问
  数据组织	通过指针或引用间接访问	直接通过变量名访问
  灵活性	支持动态调整大小	固定大小（编译时确定）

• 时间复杂度比较

  操作	堆（Heap）	栈（Stack）
  插入	O(log n)	O(1)
  删除	O(log n)	O(1)
  查找极值	O(1)	不支持
  随机访问	不支持	不支持

2. 系统内存层面

特性	堆（Heap）	栈（Stack）
内存分配	动态分配（手动malloc/free或自动GC）	自动分配（函数调用时由编译器管理）
生命周期	由程序员控制（或垃圾回收机制）	随函数调用自动创建/销毁
访问速度	较慢（需寻址）	极快（直接操作栈指针）
内存碎片	可能产生碎片	无碎片（连续存储）
大小限制	受系统内存限制（可很大）	较小（通常几MB，可能栈溢出）

说明

• 后面的数据结构以C语言的方式实现需要复用大量的代码，所以我会用Cpp语言来实现

2.3二叉搜索树🌳

• 概念与特征：二叉搜索树又称为二叉排序树，它可能是一颗空树，也可能是具有以下性质的二叉树

  • 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值【左小】
  • 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值【右大】
  • 它的左右子树也分别为二叉搜索树

• 核心性质🔑

  性质	说明
  有序性	通过左小右大的规则，保证数据的有序排列
  递归结构	每个子树都是独立的二叉搜索树，具有相同的性质
  动态维护	支持高效的动态插入、删除和查找操作

• 应用模型📊

  1. Key模型

  • 用途：判断值在不在的模型
  • 特点：只关注键的存在性，不存储额外信息

  2. Key/Value模型

  • 用途：通过key查找对应的value的模型【结构上称为键值对】
  • 实际应用：
  • 身份验证：刷身份证进高铁时，身份证就相当于键，票的信息就相当于值
  • 翻译系统：中文翻译为英文时就相当于一个键值对
  • 统计计数：统计水果个数等需要计数的场景

• ⚠️修改规则

  • 搜索树中的Key是不能修改的
  • 如果是key/value模型中的搜索树，可以修改value，但不能修改Key
  • 修改Key会破坏搜索树的结构完整性

下面将实现一个key/value模型的二叉搜索树

核心代码⚙️

#pragma once
#include <string.h>
#include <iostream>
using namespace std; // 实际开发中不使用

// 数据节点
template<class K, class V>
struct BSTNode
{
    // 构造函数
    BSTNode(const pair<K, V>& kv)
        : _kv(kv)
        , _left(nullptr)
        , _right(nullptr)
    {

    }

    pair<K, V> _kv; // kv键值对
    BSTNode<K, V>* _left; // 左孩子
    BSTNode<K, V>* _right; // 右孩子
};

// 数据结构
template<class K, class V>
class BSTree
{
    typedef BSTNode<K, V> Node;
public:
    bool Insert(const pair<K, V>& kv)
    {
        // 如果还没有创建根节点
        if (_root  nullptr)
        {
            _root = new Node(kv);
            return true;
        }

        Node* cur = _root;
        Node* parent = nullptr;
        // 找位置
        while (cur)
        {
            parent = cur;
            // 对比关键字来排
            if (kv.first > cur->_kv.first)
            {
                cur = cur->_right;
            }
            else if(kv.first < cur->_kv.first)
            {
                cur = cur->_left;
            }
            else
            {
                return false; // 关键字已存在
            }
        }

        if (kv.first > parent->_kv.first)
        {
            parent->_right = new Node(kv);
        }
        else
        {
            parent->_left = new Node(kv);
        }

        return true;
    }

    // 查找,如果找到,返回value值
    V Find(const K& key)
    {
        Node* cur = _root;
        while (cur)
        {
            if (key < cur->_kv.first)
            {
                cur = cur->_left;
            }
            else if (key > cur->_kv.first)
            {
                cur = cur->_right;
            }
            else
            {
                // 找到了对应的键
                return cur->_kv.second;
            }
        }

        cout << "non-existent key!" << endl;
        return V(); // 默认构造
    }

    // 删除
    bool Erase(const K& key)
    {
        Node* cur = _root;
        Node* parent = nullptr;
        while (cur)
        {
            if (key < cur->_kv.first)
            {
                parent = cur;
                cur = cur->_left;
            }
            else if (key > cur->_kv.first)
            {
                parent = cur;
                cur = cur->_right;
            }
            else
            {
                // 找到了对应的关键字

                if (cur->_left  nullptr)
                {
                    if (cur  _root) // parent为nullptr的情况
                    {
                        _root = cur->_right;
                    }
                    else
                    {
                        if (cur  parent->_left)
                            parent->_left = cur->_right;
                        else
                            parent->_right = cur->_right;
                    }

                    delete cur;
                }
                else if (cur->_right  nullptr)
                {
                    if (cur  _root)
                    {
                        _root = cur->_left;
                    }
                    else
                    {
                        if (cur  parent->_left)
                            parent->_left = cur->_left;
                        else
                            parent->_right = cur->_left;
                    }

                    delete cur;
                }
                // 如果左右子树都存在,我们选择取左子树的最大值作为新的cur节点(当然使用右子树的最小值也可以)
                // 当然只需要交换值就行了(不删除cur而是删除leftMax这样操作更方便)
                else
                {
                    Node* leftParent = cur;
                    Node* leftMax = cur->_left;
                    while (leftMax->_right)
                    {
                        leftParent = leftMax;
                        leftMax = leftMax->_right;
                    }

                    cur->_kv = leftMax->_kv;
                    if (leftParent  cur)
                        leftParent->_left  leftMax->_left; // leftMax一定没有右子树了
                    else
                        leftParent->_right  leftMax->_left;

                    delete leftMax; // 将交换的子树指向的空间清除
                }
                return true; // 已经将对应的值删除
            }
        }

        return false; // 如果_root为空或者没有对应的健,就返回false
    }

    // 中序遍历,实现二叉搜索树有序遍历的核心
    void InOrder()
    {
        _InOrder(_root);
    }
private:
    Node* _root = nullptr;

    // 中序遍历的子函数
    void _InOrder(Node* node)
    {
        if (node  nullptr)
        {
            return;
        }

        _InOrder(node->_left); // 左
        cout << node->_kv.first << ":" << node->_kv.second << endl; // 根
        _InOrder(node->_right); // 右
    }
};

增删查✂️

操作	函数	时间复杂度	说明
✅ 增	Insert	O(log n)	从根节点开始，通过比较关键字大小向下搜索至正确位置，插入新节点。在平衡情况下，树高为log n
❌ 删	Erase	O(log n)	从根节点开始，通过比较关键字大小向下搜索至目标节点。删除后，若需替换，则继续向下搜索左子树的最大值或右子树的最小值。在平衡情况下，树高为log n
🔍 查	Find	O(log n)	从根节点开始，通过比较关键字大小向下搜索至目标节点。在平衡情况下，树高为log n

遍历

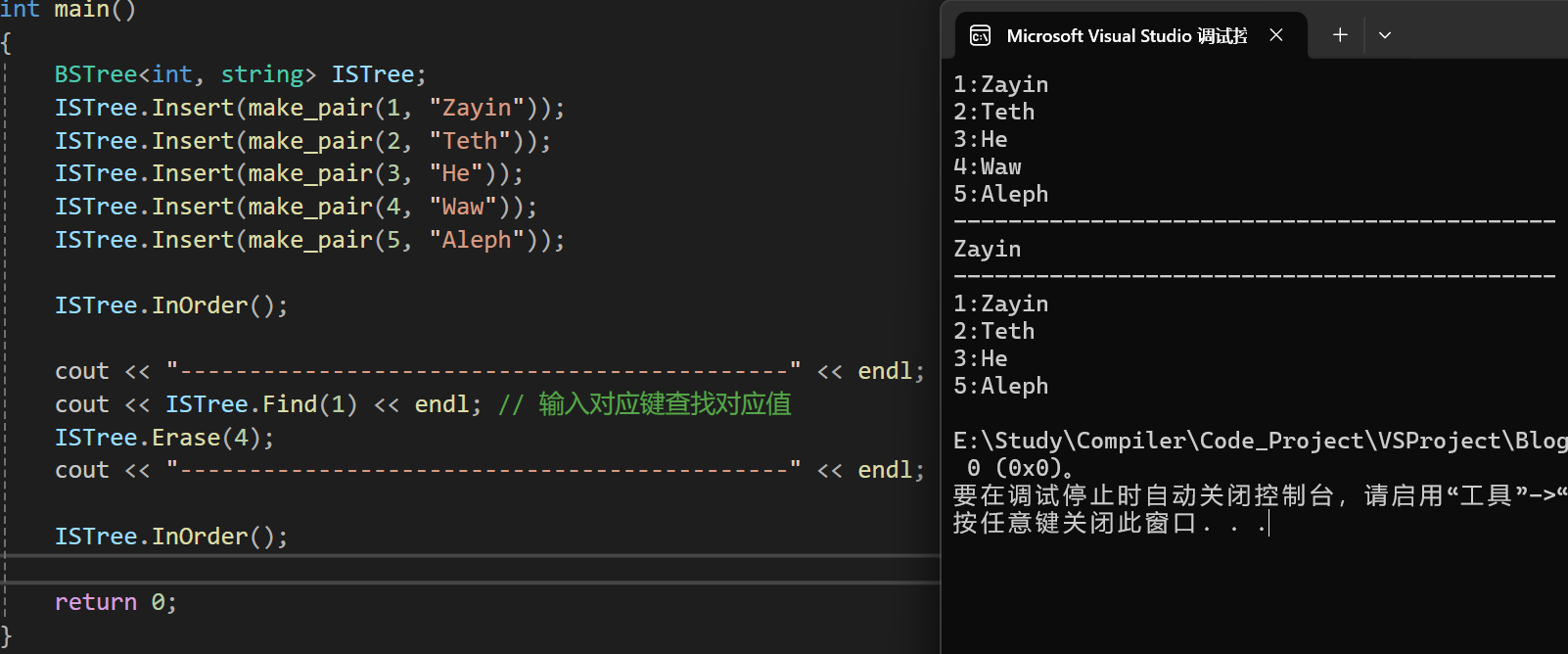
• 中序遍历(InOrder)：中序遍历是左 =》根 =》右的遍历顺序，在二叉搜索树中可以实现按Key从小到大的顺序遍历数据

总结：二叉搜索树的优势与应用💡

优势	说明
高效搜索	在平衡情况下，搜索效率为O(log n)，远优于线性搜索
动态维护有序性	插入删除操作后自动维持数据的有序性
灵活的数据结构	支持Key模型和Key/Value模型，适应不同应用场景
中序遍历有序	天然支持有序遍历，无需额外排序操作

• 实际应用场景

1. 数据库索引
   • 场景：数据库中的B+树索引基于二叉搜索树原理
   • 优势：快速定位记录，提高查询效率
2. 字典和映射
   • 场景：编程语言中的map、dictionary等数据结构
   • 实现：基于Key/Value模型的二叉搜索树变种(一般是红黑树)
3. 文件系统
   • 场景：操作系统中的目录结构
   • 特点：天然的多级目录树形结构
4. 自动补全系统
   • 场景：搜索引擎、IDE的代码补全
   • 原理：构建抽象语法树进行前缀搜索和范围查询
5. 区间查询
   • 场景：查找某个范围内的所有数据
   • 实现：利用中序遍历的有序特性

注意事项⚠️

• 平衡性问题：当数据有序或接近有序时，树可能退化为链表，搜索效率降为O(n)
• 解决方案：需要使用平衡二叉搜索树（如AVL树、红黑树）来保证性能稳定性
• 键的唯一性：二叉搜索树要求键是唯一的，重复键需要特殊处理

2.4AVLTree(平衡树)⚖️

• 概念：由于搜索树数据有序时的糟糕查找效率，所以在二叉搜索树的基础上增加了平衡因子的概念，通过旋转操作自动维持树的平衡，确保搜索效率始终保持在O(log n)级别，这种数据结构就成为平衡树(AVLTree，即优化的二叉搜索树)。

• 核心性质🔑：

  性质	说明
  平衡因子约束	每个节点的左右子树高度差的绝对值不超过1
  严格平衡性	通过旋转操作强制维持树的近似完全平衡
  高效搜索保证	树的高度始终保持在O(log n)级别
  自动调整机制	插入删除操作后自动检测并修复不平衡

AVLTree如何保持平衡?

平衡因子

• 定义：平衡因子 = 节点右子树高度 - 节点左子树高度
• 值域：-1，0，1
• 机理与作用：平衡因子是用来判断搜索树是否平衡的变量，是为了方便我们实现平衡树接口的一个变量，在一棵平衡树中，当它的值在值域范围内时，就代表该树平衡，不需要其余操作；当它的取值在范围外，就代表这棵树不平衡，需要进行旋转操作来保持树的平衡

旋转策略：解决插入删除时对应情况的核心接口

• 插入删除时对应的情况：

  • 情况1：新节点插入较高右子树的右侧
  • 情况2：新节点插入较高左子树的左侧
  • 情况3：新节点插入较高左子树的右侧(即内侧)
  • 情况4：新节点插入较高右子树的左侧(即内侧)

• 作用与分类：旋转是用来保持树平衡的接口，实现树平衡的旋转接口一共有四种

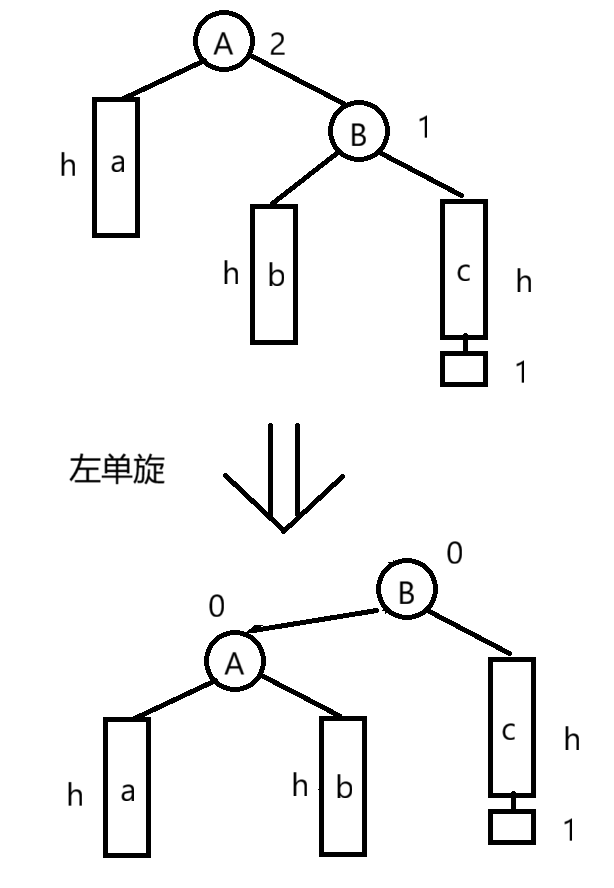
  1. 左单旋：

     • 触发条件： 父节点bf=2，右孩子bf=1（外侧，即情况1）
     • 操作：将父节点向左方向旋转

     

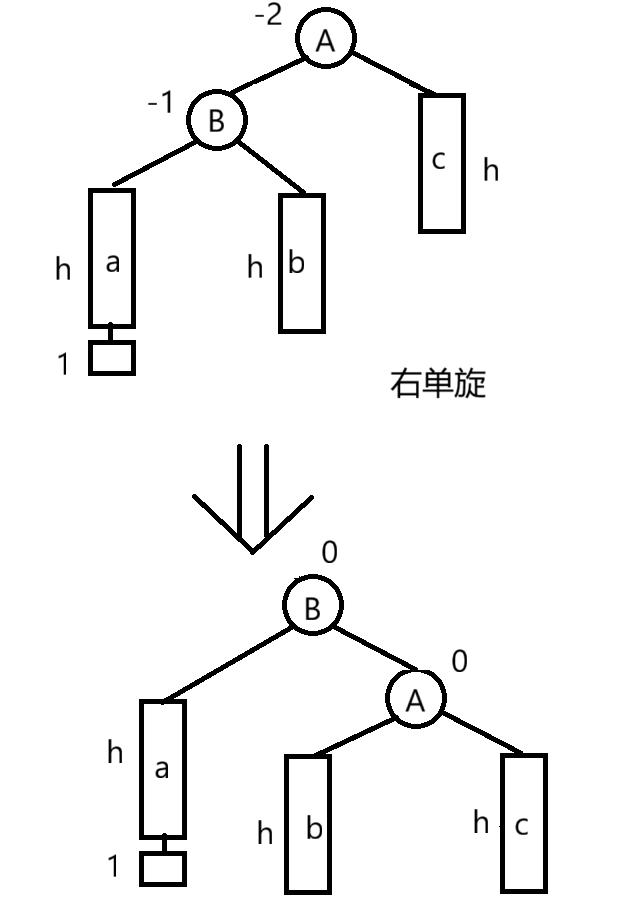
  2. 右单旋：

     • 触发条件：父节点bf=-2，左孩子bf=-1（外侧，即情况2）
     • 操作：将父节点向右方向旋转

     

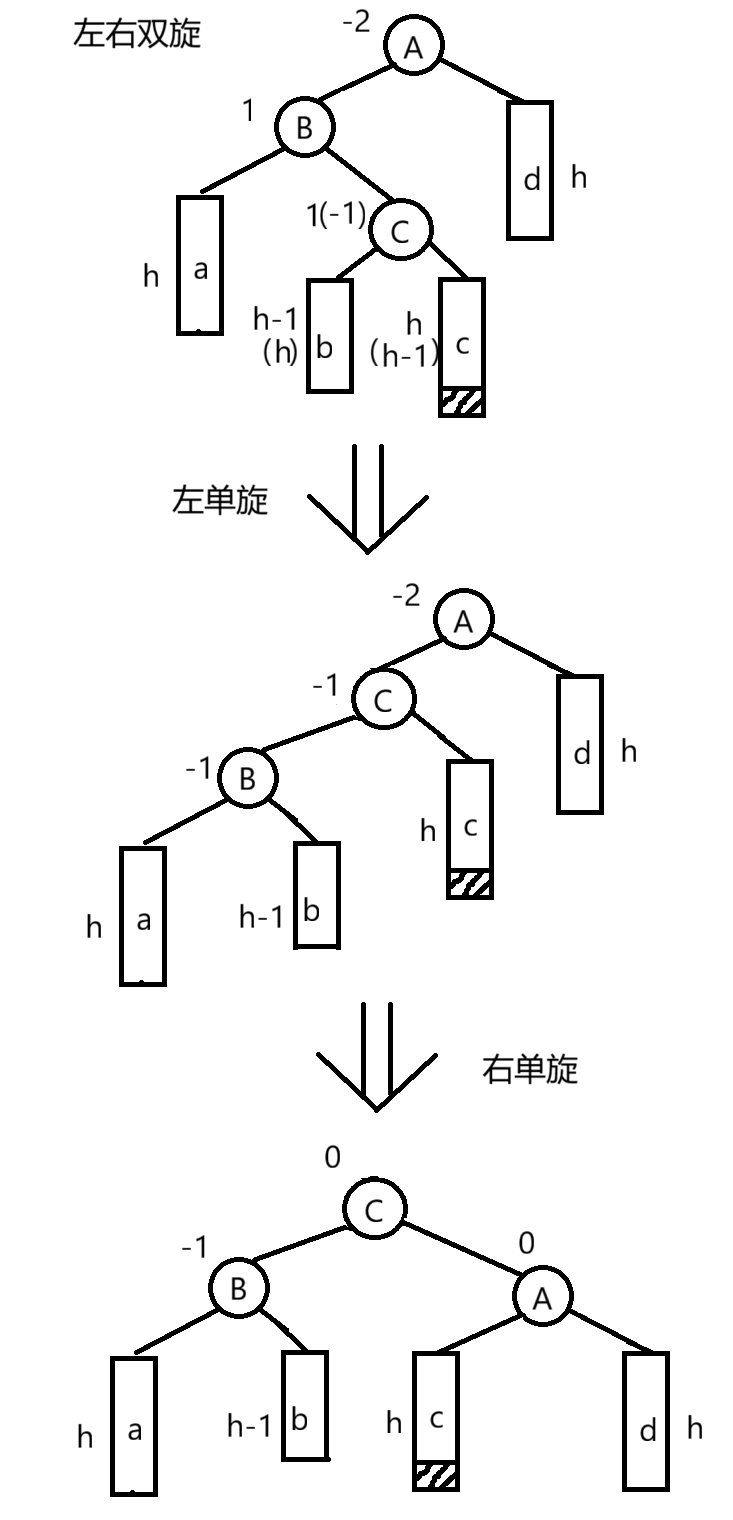
  3. 左右双旋：

     • 触发条件：父节点bf=-2，左孩子bf=1（内侧，即情况3）
     • 操作：先对根节点的左子树进行一次左单旋，然后对根节点自身进行一次右单旋【复用左单旋，右单旋的代码】
     • 结果：有三种情况
       1. 如果新增节点在左子树右树的右边，调整完后，左子树的平衡因子为-1，根和右子树的平衡因子为0
       2. 如果新增节点在左子树右树的左边，调整完后，右子树的平衡因子为1，左子树和根的平衡因子为0
       3. 如果新增节点为这棵树的第三个节点，调整完后根，左子树以及右子树的平衡因子均赋值为0

     

  4. 右左双旋：

     • 触发条件：父节点bf=2，右孩子bf=-1（内侧，即情况4）
     • 操作：先对根节点的左子树进行一次左单旋，然后对根节点自身进行一次右单旋【复用左单旋，右单旋的代码】
     • 结果：有三种情况
       1. 如果新增节点在右子树左树的右边，调整完后，左子树的平衡因子为-1，根和右子树的平衡因子为0
       2. 如果新增节点在右子树左树的左边，调整完后，右子树的平衡因子为1，左子树和根的平衡因子为0
       3. 如果新增节点为这棵树的第三个节点，调整完后根，左子树以及右子树的平衡因子均赋值为0

     

核心代码⚙️

#pragma once
#include <iostream>
#include <string.h>
using namespace std;

// 数据节点
template<class K, class V>
struct AVLTNode
{
    AVLTNode(const pair<K, V> kv)
        : _kv(kv)
        , _parent(nullptr)
        , _right(nullptr)
        , _left(nullptr)
        , _bf(0)
    {

    }

    pair<K, V> _kv;
    AVLTNode* _left;
    AVLTNode* _right;
    AVLTNode* _parent; // 定义一个父节点指针,方便进行平衡操作

    int _bf; // 平衡因子
};

template<class K, class V>
class AVLTree
{
    typedef AVLTNode<K, V> Node;
public:
    // 插入
    bool Insert(const pair<K, V>& kv)
    {
        if (_root  nullptr)
        {
            _root = new Node(kv);
            return true;
        }

        Node* cur = _root;
        Node* parent = nullptr;
        while (cur)
        {
            parent = cur;
            if (kv.first > cur->_kv.first)
            {
                cur = cur->_right;
            }
            else if (kv.first < cur->_kv.first)
            {
                cur = cur->_left;
            }
            else
            {
                return false; // 说明对应的关键字已存在
            }
        }

        cur = new Node(kv); // 将cur复用为指向新创建空间的指针
        if (kv.first > parent->_kv.first)
        {
            parent->_right = cur;
            cur->_parent = parent;
        }
        else
        {
            parent->_left = cur;
            cur->_parent = parent;
        }

        // 逐个检查父节点的平衡因子 
        while (parent)
        {
            // 因为前面增加了新节点,所以要修改平衡因子
            if (cur  parent->_left)
                --parent->_bf;
            else if (cur  parent->_right)
                ++parent->_bf;

            // 如果bf为0,说明树的高度没变,保持平衡
            if (parent->_bf  0)
            {
                break;
            }
            // 如果bf为1,说明树的高度改变,继续向上检查平衡因子
            else if (abs(parent->_bf)  1)
            {
                cur = parent;
                parent = parent->_parent;
            }
            // 如果bf为2,说明二叉搜索树不平衡,需要旋转处理
            else if (abs(parent->_bf)  2)
            {
                // 查看父节点bf与子节点bf的符号关系
                if (parent->_bf  -2)
                {
                    // 左同侧,右单旋
                    if (cur->_bf  -1) {
                        RightRotate(parent);
                    }
                    // 左内测,左右双旋
                    else {
                        RotateLR(parent);
                    }
                }
                else
                {
                    // 右同侧,左单旋
                    if (cur->_bf  1) {
                        LeftRotate(parent);
                    }
                    // 右内侧,右左双旋
                    else {
                        RotateRL(parent);
                    }
                }
                break; // 优化设置,当平衡树进行平衡操作后,那么该树一定平衡,所以不用继续向上检查了
            }
        }

        return true;
    }

    size_t Height()
    {
        return _Height(_root);
    }

    // 如果要使用这个函数,那么说明平衡树可能会因外界影响而导致不平衡,这不能从bf看出,因为bf由内部的Insert函数决定
    bool IsBalance()
    {
        return _IsBalance(_root);
    }

    // 中序遍历
    void InOrder()
    {
        _InOrder(_root);
    }

private:
    Node* _root = nullptr;

    // 找到左支和右支中高度最高的那颗子树，用递归即可
    size_t _Height(Node* node)
    {
        if (node  nullptr)
            return 0;

        size_t HeightLeft = _Height(node->_left);
        size_t HeightRight = _Height(node->_right);

        return HeightLeft >= HeightRight ? HeightLeft + 1 : HeightRight + 1; // 默认左树
    }

    bool _IsBalance(Node* node)
    {
        // 直接返回true是为了下面return时候的_Isbalance函数也能满足true1的条件
        if (node  nullptr)
            return true;

        // 用int防止下面相减数据为负数导致变为无符号最大值
        int HeightLeft = _Height(node->_left);
        int HeightRight = _Height(node->_right);

        // 根节点,左子树,右子树都要满足平衡
        return abs(HeightLeft - HeightRight) <= 1
            && _IsBalance(node->_left)
            && _IsBalance(node->_right);
    }

    void _InOrder(Node* node)
    {
        if (node  nullptr)
            return;

        _InOrder(node->_left); // 左
        cout << node->_kv.first << ":" << node->_kv.second << endl; // 根
        _InOrder(node->_right); // 右
    }

    // 左单旋
    void LeftRotate(Node* targetParent)
    {
        // 需要调整的节点
        Node* pParent = targetParent->_parent;
        Node* subR = targetParent->_right;
        Node* subRLeft = subR->_left;

        if (targetParent  _root) {
            _root = subR;
        }
        else {
            if (pParent->_left  targetParent) {
                pParent->_left = subR;
            }
            else {
                pParent->_right = subR;
            }
        }
        subR->_parent = pParent;

        targetParent->_parent = subR;
        subR->_left = targetParent;
        targetParent->_right = subRLeft;
        if (subRLeft)
        {
            subRLeft->_parent = targetParent;
        }

        // 更新平衡因子
        subR->_bf = targetParent->_bf = 0;
    }

    // 右单旋
    void RightRotate(Node* targetParent)
    {
        Node* pParent = targetParent->_parent;
        Node* subL = targetParent->_left;
        Node* subLRight = subL->_right;

        if (targetParent  _root) {
            _root = subL;
        }
        else {
            if (pParent->_left = targetParent) {
                pParent->_left = subL;
            }
            else {
                pParent->_right = subL;
            }
        }
        subL->_parent = pParent;

        targetParent->_parent = subL;
        subL->_right = targetParent;
        targetParent->_left = subLRight;
        if (subLRight)
        {
            subLRight->_parent = targetParent;
        }

        // 更新平衡因子
        subL->_bf = targetParent->_bf = 0;
    }

    // 左右双旋
    void RotateLR(Node* targetParent)
    {
        // 因为在左单旋和右单旋函数中尾部调整了平衡因子,而双旋会导致平衡因子不都变成0,所以还要手动调整平衡因子
        Node* subL = targetParent->_left;
        Node* subLR = subL->_right;
        int bf = subLR->_bf; // 因为bf可能是1或者-1,接下来调整平衡因子需要考虑

        LeftRotate(subL);
        RightRotate(targetParent);

        // 左树高
        if (bf  -1)
        {
            subL->_bf = 0;
            subLR->_bf = 0;
            targetParent->_bf = 1;
        }
        // 右树高
        else if (bf  1)
        {
            subL->_bf = -1;
            subLR->_bf = 0;
            targetParent->_bf = 0;
        }
        // 还有一种特殊情况,只有targetParent,subL和subLR三个节点的情况,也就是subLR作为第一次插入在内侧的节点
        else
        {
            subL->_bf = subLR->_bf = targetParent->_bf = 0;
        }
    }

    // 右左双旋
    void RotateRL(Node* targetParent)
    {
        // 类似于左右双旋
        Node* subR = targetParent->_right;
        Node* subRL = subR->_left;
        int bf = subRL->_bf; 

        RightRotate(subR);
        LeftRotate(targetParent);

        // 左树高
        if (bf  -1)
        {
            subR->_bf = 1;
            subRL->_bf = 0;
            targetParent->_bf = 0;
        }
        // 右树高
        else if (bf  1)
        {
            subR->_bf = 0;
            subRL->_bf = 0;
            targetParent->_bf = -1;
        }
        else
        {
            subR->_bf = subRL->_bf = targetParent->_bf = 0;
        }
    }
};

• 上述代码中没有实现删除代码，但是删除代码的逻辑和插入的相似
• 测试样例：

总结：AVL树的优势与应用💡

• AVL树的优势

优势	说明
严格平衡保证	保证树的高度始终为O(log n)，提供稳定的查询性能
高效查询操作	搜索、插入、删除操作的时间复杂度均为O(log n)
自动平衡维护	插入删除后自动旋转调整，无需手动维护平衡
有序数据存储	保持二叉搜索树性质，支持有序遍历

• AVL树的应用

1. 数据库索引
   • 场景：需要快速查找和范围查询的数据库系统
   • 优势：稳定的O(log n)查询性能，适合频繁查询场景
2. 内存数据库
   • 实现：Redis等内存数据库使用类似AVL的平衡树结构
   • 特点：高效的内存数据组织和快速检索
3. 文件系统
   • 场景：文件目录结构管理
   • 应用：维护文件和目录的快速查找和遍历
4. 编译器实现
   • 符号表管理：存储变量、函数等符号信息
   • 优势：快速查找符号定义和类型信息
5. 网络路由表
   • 场景：路由器中的IP地址查找
   • 实现：使用平衡树高效管理路由规则
6. 实时系统
   • 需求：保证最坏情况下的性能
   • 优势：AVL树的严格平衡性满足实时性要求

2.5红黑树🔴⚫🌳

• 概念与特征：红黑树是一种自平衡的二叉搜索树，它在每个节点上增加了一个存储位表示节点的颜色（红色或黑色），通过颜色约束来维持树的近似平衡

• 核心性质🔑

  性质	说明
  近似平衡	通过颜色约束保证最长路径不超过最短路径的两倍
  高效维护	插入删除操作的旋转次数明显少于AVL树
  性能均衡	在查询效率和维护成本之间取得良好平衡
  广泛应用	被众多编程语言和系统选作标准关联容器的底层实现

对比AVL树，红黑树如何保持平衡

颜色

• 为了达成类似AVL树的平衡效果，降低设计的复杂度并且防止频繁的旋转导致效率降低，红黑树引入了红黑两种颜色来控制节点，以及对应的颜色规则

• 红黑树的颜色规则：

  • 每个节点要么是红色，要么是黑色
  • 根节点必须是黑色
  • 所有叶子节点（NIL节点）都是黑色
  • 不能有两个连续的红色节点
  • 从任一节点到其每个叶子节点的所有路径都包含相同数量的黑色节点

• 总结：1.根节点是黑色的 2.没有连续的红节点 3.每条路径都有相同数量的黑节点

• 效率：

  • 最长的路径：一黑一红相间，效率为O(logN)

  • 最短的路径：全黑，效率为2 * O(logN)

  • 理论上来说，红黑树的效率比AVL树的效率略低，但是因为硬件的运算足够快，所以在事实上基本上没有差异，因为logN是已经足够小了

  • 但是插入删除同样节点红黑树比AVL树旋转更少，因为AVL树更严格的平衡实际上是通过多旋转达到的。况且红黑树在实现上更容易控制，所以实际红黑树得到了更广泛的应用（红黑树相比AVL树的最大优势就是插入删除时能够大大减少旋转的次数）

红黑树中的旋转

• 红黑树中简化了旋转操作，对比AVL树，红黑树只有两种旋转，左单旋和右单旋，当然了，红黑树中旋转操作也是为了处理插入删除时遇见的几种情况

• 作用及分类：

  1. 左单旋：

     • 触发条件：cur节点为右外侧红节点，parent为红节点，uncle节点存在且为黑节点，或者uncle节点不存在
     • 作用：旋转并调整节点的颜色，使这棵树同时满足不出现连续红节点和黑节点个数相同的要求

     

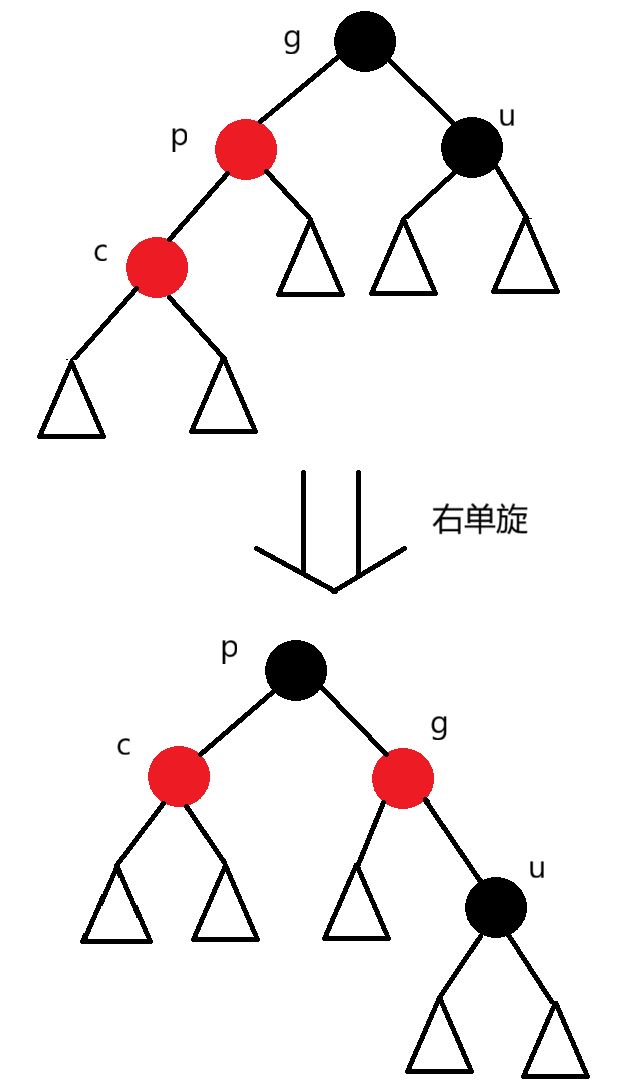
  2. 右单旋：

     • 触发条件：cur节点为左外侧红节点，parent为红节点，uncle节点存在且为黑节点，或者uncle节点不存在
     • 作用：旋转并调整节点的颜色，使这棵树同时满足不出现连续红节点和黑节点个数相同的要求

     

红黑树中插入与删除时对应的情况

• 情况1：cur为红节点，parent为红节点，grandfather为黑节点，uncle节点存在且为红节点【不需要旋转操作】

  • 处理：
  1. 使p和u节点变为黑节点，将g(非根节点时)变成红节点
  2. 如果g节点(设为新的cur节点，看作是新插入g节点)的父节点也是红节点，若新cur节点也有一个u节点且它为红节点，那么就可以重复上述操作，然后再继续向上处理【隔两个元素向上处理】

  

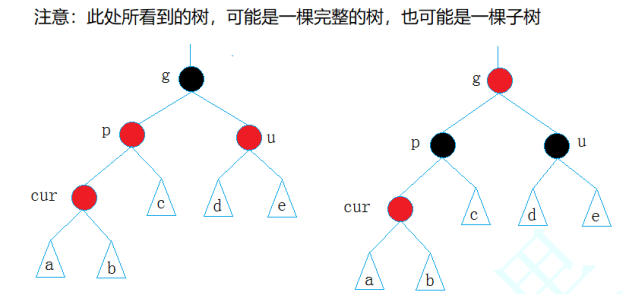
• 情况2：cur为红色外侧节点，parent为红节点，grandfather为黑节点，且uncle节点存在且为黑节点或者说uncle节点不存在

  • 处理：
    1. uncle节点不存在：那么cur节点一定为新增节点(若cur为新插入的红节点，同时uncle节点存在且为黑节点，那么grandparent节点的两个子树的黑节点个数会不相同)
       • 进行单旋操作，然后将新的父节点变成黑节点，将原来的g节点变成红节点
    2. uncle节点存在，那么cur节点一定不是新增节点(同上，若cur为新增红节点，那么uncle节点不可能为黑节点)
       • 进行单旋操作，然后将新的父节点变成黑节点，将原来的g节点变成红节点，u节点的颜色不变

• 情况3：cur为红色内侧节点，parent为红节点，grandfather为黑节点，且uncle节点存在且为黑节点或者说uncle节点不存在

  • 处理：

  1. uncle节点不存在：

     • 先进行单旋操作，直接转换为情况2 also 进行双旋操作，原来的cur节点成了新的父节点，颜色变成黑色，原来g节点的颜色变成红色【⚠️第一次单旋不变色】

  2. uncle节点存在：

     • 先进行单旋操作，直接转换为情况2 also 进行双旋操作，原来的cur节点成了新的父节点，颜色变成黑色，原来g节点的颜色变成红色，u节点不变色【⚠️第一次单旋不变色】

• 注意事项⚠️：以上任何情况中，若g为非根节点，那么就不会改变每个分支中黑节点个数，只有当调整至g为根节点时才能增加每个分支中黑节点的个数

核心代码⚙️

#pragma once
#include <iostream>
#include <string.h>
using namespace std;

// 红黑树通过着色方式对树的高度进行限制，确保不会有一条路径比其他路径长出两倍(虽然不如AVL树的绝对平衡，但是更常用和好用,简化了AVL树的旋转操作)
// 规则：
// 1.每个节点不是红色的就是黑色的
// 2.根节点是黑色的
// 3.如果一个节点是红色的，那么它的两个孩子节点都是黑色的
// 4.对于每个节点，从该节点到其后代叶节点的简单路径上，均包含相同数目的黑色节点
// 5.每个叶子节点的两个空子节点都是黑色的（方便标记路径）

// 总结:1.根节点是黑色的   2.没有连续的红节点   3.每条路径都有相同数量的黑节点

// 红黑树的颜色
enum Color
{
    red,
    black,
};

// 数据节点
template<class K, class V>
struct RBTNode
{
    // 默认给黑色作为节点的默认颜色
    RBTNode(const pair<K, V>& kv, Color color = black)
        : _kv(kv)
        , _left(nullptr)
        , _right(nullptr)
        , _parent(nullptr)
        , _color(color)
    {

    }

    pair<K, V> _kv;
    RBTNode* _left;
    RBTNode* _right;
    RBTNode* _parent; // 父节点指针,方便红黑树进行平衡操作

    Color _color; // 节点颜色
};

// 双向迭代器
template<class K, class V, class Ref, class Ptr>
struct __TreeIterator // 对红黑树的节点指针进行一定程度的封装而达成迭代器的效果
{
    typedef RBTNode<K, V> Node;
    typedef __TreeIterator<K, V, Ref, Ptr> Self;
    Node* _node;

    __TreeIterator(Node* node)
        : _node(node)
    {

    }

    Ref operator* ()
    {
        return _node->_data; // 返回键或者键值对(可修改)
    }

    Ptr operator->()
    {
        return &_node->_data;
    }

    bool operator!=(const Self& s)
    {
        return _node != s._node;
    }

    bool operator(const Self& s)
    {
        return _node  s._node;
    }

    // 前++
    Self& operator++()
    {
        // 1.如果右树不为空,就找右树的最左子树
        if (_node && _node->_right)
        {
            Node* subLeft = _node->_right;
            while (subLeft && subLeft->_left)
            {
                subLeft = subLeft->_left;
            }
            _node = subLeft;
        }
        // 2.如果无右树,就向上找,且如果该节点为父节点的右树,那么就需要更新节点位置,继续往上找,直到该节点为父节点的左树为止
        else
        {
            Node* cur = _node;
            Node* parent = cur->_parent;
            if (parent && cur  parent->_right)
            {
                cur = parent;
                parent = parent->_parent;
            }
            _node = parent; // 最后将_node更新到父节点
        }
        return *this; // 返回作为迭代器的自身
    }

    // 前--
    Self& operator--()
    {
        // 1.如果左树不为空,就找左树的最右子树
        if (_node && _node->_left)
        {
            Node* subRight = _node->_left;
            while (subRight && subRight->_left)
            {
                subRight = subRight->_left;
            }
            _node = subRight;
        }
        // 2.如果无左树,就向上找,且如果该节点为父节点的左树,那么就需要更新节点位置,继续往上找,直到该节点为父节点的右树为止
        else
        {
            Node* cur = _node;
            Node* parent = cur->_parent;
            if (parent && cur  parent->_left)
            {
                cur = parent;
                parent = parent->_parent;
            }
            _node = parent; // 最后将_node更新到父节点
        }
        return *this; // 返回作为迭代器的自身
    }
};

// 数据结构
template<class K, class V>
class RBTree
{
    typedef RBTNode<K, V> Node;
public:
    typedef __TreeIterator<K, V, pair<K, V>&, pair<K, V>*> iterator; // 迭代器
    typedef __TreeIterator<K, V, const pair<K, V>&, const pair<K, V>*> const_iterator; // 常迭代器

    bool Insert(const pair<K, V>& kv)
    {
        // 按搜索树的规则插入
        if (_root  nullptr)
        {
            _root = new Node(kv, black);
            return true;
        }

        Node* cur = _root;
        Node* parent = nullptr;
        while (cur)
        {
            parent = cur;
            if (kv.first > cur->_kv.first)
            {
                cur = cur->_right;
            }
            else if (kv.first < cur->_kv.first)
            {
                cur = cur->_left;
            }
            else
            {
                // 对应键已存在
                return false;
            }
        }

        cur = new Node(kv, red); // 复用cur节点,且让它为红节点,如果parent为红节点可以进行调整,但是如果设置为黑节点可能导致每条路径上的黑节点个数不相同
        cur->_parent = parent;
        if (kv.first > parent->_kv.first)
        {
            parent->_right = cur;
        }
        else
        {
            parent->_left = cur;
        }

        // 红黑树核心:
        // 如果父节点存在且颜色为红色那么就要分情况进行讨论(关系四个节点:grandParent,parent,uncle和cur节点)
        while (parent && parent->_color  red)
        {
            Node* grandParent = parent->_parent; // 因为parent节点为红节点,那么grandParent一定存在
            // parent节点在左子树
            if (grandParent->_left  parent)
            {
                Node* uncle = grandParent->_right;
                // 情况1:如果uncle节点存在且为红节点(唯一增加路径上黑节点个数的方式)
                if (uncle && uncle->_color  red)
                {
                    uncle->_color = parent->_color = black;
                    grandParent->_color = red; // 如果是根节点,后续调整会将该节点转换会黑节点

                    cur = grandParent;
                    parent = cur->_parent;
                }
                // 情况2 or 情况3:如果uncle不存在或者存在时为黑节点,需要进行旋转操作
                else
                {
                    // 先单独处理情况3(cur节点在parent的内侧子树),将情况3转化为情况2(左单旋)
                    if (parent->_right  cur)
                    {
                        LeftRotate(parent);
                        swap(cur, parent); // 把cur和parent指向的空间交换(保证更新的节点正确)
                    }

                    // 情况2(cur节点时parent的外侧节点)
                    RightRotate(grandParent);
                    parent->_color = black;
                    grandParent->_color = red;

                    break; // 已满足红黑树规则,停止向上调整
                }
            }
            else if (grandParent->_right  parent)
            {
                Node* uncle = grandParent->_left;
                // 情况1
                if(uncle && uncle->_color  red)
                {
                    uncle->_color = parent->_color = black;
                    grandParent->_color = red; 

                    cur = grandParent;
                    parent = cur->_parent;
                }
                // 情况2 or 情况3
                else
                {
                    // 情况3
                    if (parent->_left  cur)
                    {
                        RightRotate(parent);
                        swap(cur, parent);
                    }

                    // 情况2
                    LeftRotate(grandParent);
                    parent->_color = black;
                    grandParent->_color = red;

                    break;
                }
            }
        }
        // 最后记得将_root重设为黑节点,防止根节点被改为红节点
        _root->_color = black; 
        return true;
    }

    void InOrder()
    {
        _InOrder(_root);
    }

private:
    Node* _root = nullptr;

    void LeftRotate(Node* targetParent)
    {
        Node* pParent = targetParent->_parent;
        Node* subR = targetParent->_right;
        Node* subRL = subR->_left;

        // 因为targetParent一定有父节点,所以不用讨论targetParent为_root的情况-->错误:因为传入的指针不一定是parent,还可能是grandParent,grandParent不一定有parent节点
        subR->_left = targetParent;
        targetParent->_parent = subR;
        if (targetParent != _root) {
            if (pParent->_left  targetParent) {
                pParent->_left = subR;
            }
            else {
                pParent->_right = subR;
            }
        }
        else {
            _root = subR;
        }
        subR->_parent = pParent;

        targetParent->_right = subRL;
        if (subRL) {
            subRL->_parent = targetParent;
        }
    }

    void RightRotate(Node* targetParent)
    {
        Node* pParent = targetParent->_parent;
        Node* subL = targetParent->_left;
        Node* subLR = subL->_right;

        // 因为targetParent一定有父节点,所以不用讨论targetParent为_root的情况
        subL->_right = targetParent;
        targetParent->_parent = subL;

        if (targetParent != _root) {
            if (pParent->_left  targetParent) {
                pParent->_left = subL;
            }
            else {
                pParent->_right = subL;
            }
        }
        else {
            _root = subL;
        }

        subL->_parent = pParent;

        targetParent->_left = subLR;
        if (subLR) {
            subLR->_parent = targetParent;
        }
    }

    void _InOrder(Node* node)
    {
        if (node  nullptr)
        {
            return;
        }

        _InOrder(node->_left); // 左
        cout << node->_kv.first << ":" << node->_kv.second << endl; // 根
        _InOrder(node->_right);// 右
    }
};

• 上述代码中没有实现删除代码，但是删除代码的逻辑和插入的相似
• 测试样例：

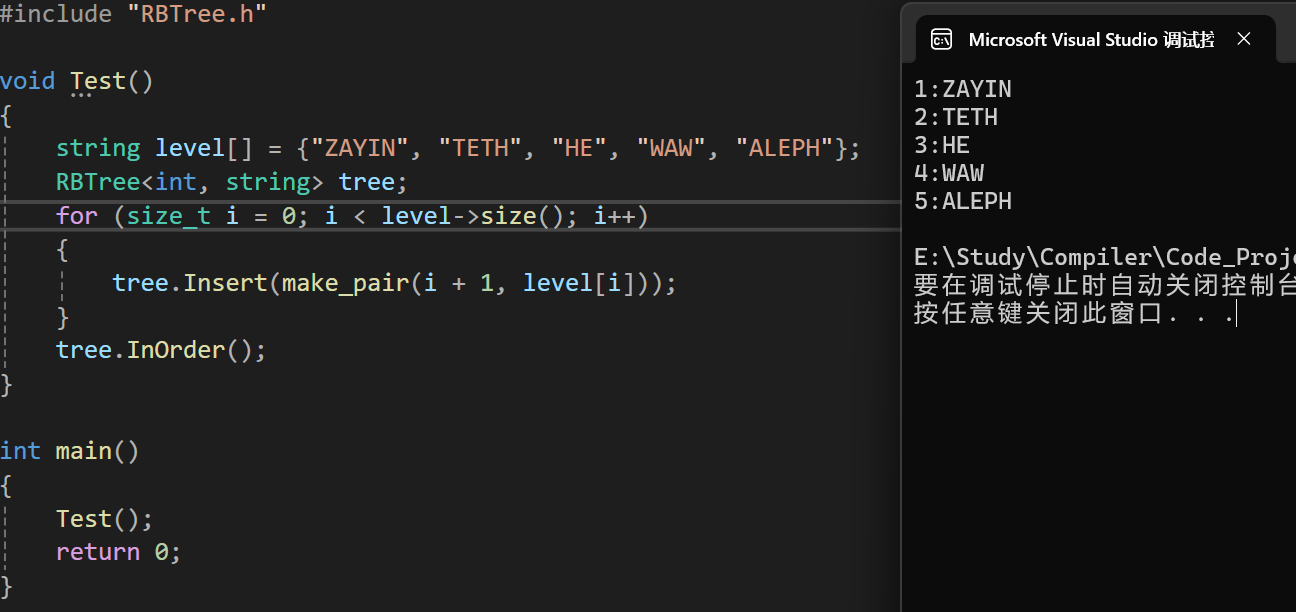
set与map

• Cpp的set与map是基于红黑树实现的，下面是使用红黑树实现的set与map的模拟代码

// map
template <class K, class V>
class map
{
public:
    // 获取T中的Key数据
    struct MapKeyOfT
    {
        const K& operator()(const pair<K, V>& kv)
        {
            return kv.first; // 返回key
        }
    };

public:
    typedef typename RBTree<K, pair<K, V>, MapKeyOfT>::iterator iterator;

    iterator begin()
    {
        return _tree.begin();
    }

    iterator end()
    {
        return _tree.end();
    }

    pair<iterator, bool> Insert(const pair<K, V>& kv)
    {
        return _tree.Insert(kv);
    }

    V& operator[](const K& key)
    {
        pair<iterator, bool> ret = _tree.Insert(make_pair<key, V()>); // 调用V的默认构造函数
        return (ret.first)->second;
    }
private:
    RBTree<K, pair<K, V>, MapKeyOfT> _tree;
};

// set
template<class K>
class set
{
public:
    struct SetKeyOfT
    {
        const K& operator()(const K& key)
        {
            return key; // 返回key
        }
    };

public:
    typedef typename RBTree<K, K, SetKeyOfT>::iterator iterator; // 编译器找不到RBTree,因为它是跨文件的模板,不能通过,要加一个typename才能找到

    iterator begin()
    {
        return _tree.begin();
    }

    iterator end()
    {
        return _tree.end();
    }

    pair<iterator, bool> Insert(const K& key)
    {
        return _tree.Insert(key);
    }

private:
    RBTree<K, K, SetKeyOfT> _tree;
};

• 测试样例：

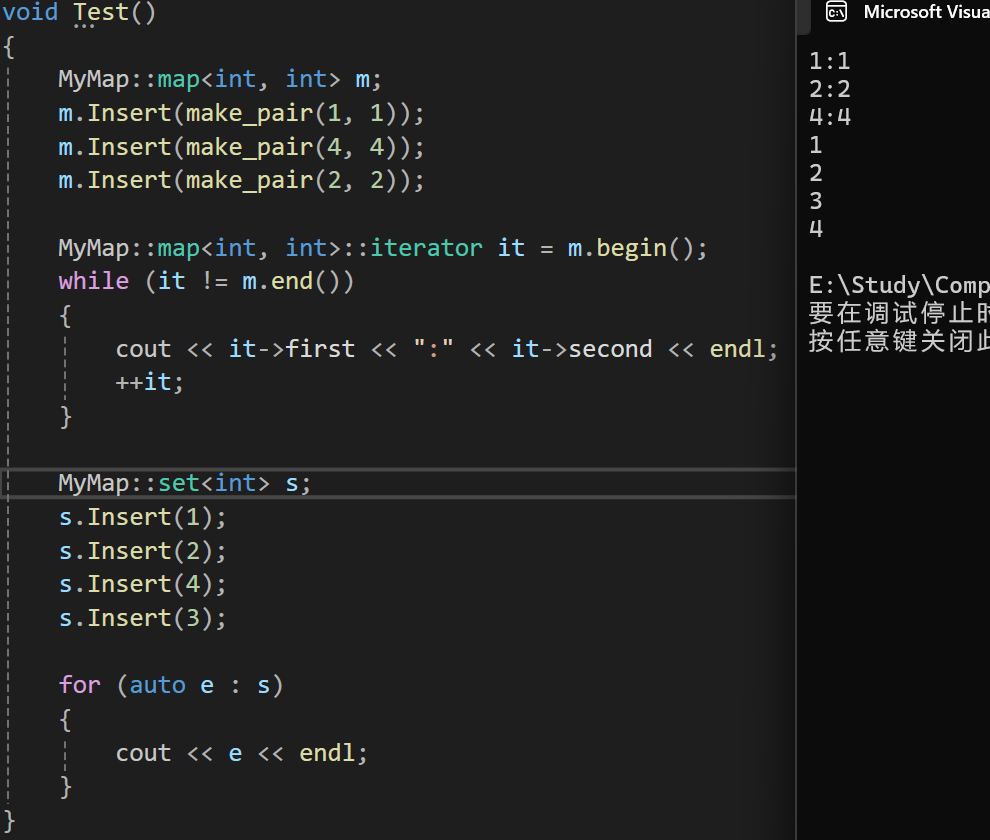
红黑树的验证

• 为了保持红黑树结构的稳定，有时还会对红黑树进行验证，验证步骤分为两步：
  1. 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
  2. 检测其是否满足红黑树的性质
• 代码：

bool IsValidRBTree()
{
    PNode pRoot = GetRoot();
    // 空树也是红黑树
    if (nullptr  pRoot)
        return true;
    // 检测根节点是否满足情况
    if (BLACK != pRoot->_color)
    {
        cout << "违反红黑树性质二：根节点必须为黑色" << endl;
        return false;
    }
    // 获取任意一条路径中黑色节点的个数
    size_t blackCount = 0;
    PNode pCur = pRoot;
    while (pCur)
    {
        if (BLACK  pCur->_color)
        {
            blackCount++;
            pCur = pCur->_pLeft;
        }
    }
    // 检测是否满足红黑树的性质，k用来记录路径中黑色节点的个数
    size_t k = 0;
    return _IsValidRBTree(pRoot, k, blackCount);
}

bool _IsValidRBTree(PNode pRoot, size_t k, const size_t blackCount)
{
    //走到null之后，判断k和black是否相等
    if (nullptr  pRoot)
    {
        if (k != blackCount)
        {
            cout << "违反性质四：每条路径中黑色节点的个数必须相同" << endl;
            return false;
        }
        return true;
    }
    // 统计黑色节点的个数
    if (BLACK  pRoot->_color)
        k++;
    // 检测当前节点与其双亲是否都为红色
    PNode pParent = pRoot->_pParent;
    if (pParent && RED  pParent->_color && RED  pRoot->_color)
    {
        cout << "违反性质三：没有连在一起的红色节点" << endl;
        return false;
        }
    return _IsValidRBTree(pRoot->_pLeft, k, blackCount) &&
    _IsValidRBTree(pRoot->_pRight, k, blackCount);
 }

总结：红黑树的优势与应用💡

优势	说明
综合性能优秀	在插入、删除、查询操作间取得最佳平衡
维护成本低	相比AVL树，旋转操作更少，适合频繁更新的场景
工业级标准	被C++ STL、Java HashMap等广泛采用
理论保证	保证最长路径不超过最短路径的两倍，性能可预测

• 实际应用场景

1. C++ STL容器
   • 场景：std::map、std::set的底层实现
   • 优势：提供稳定的对数时间复杂度保证
2. Java集合框架
   • 场景：TreeMap、TreeSet的实现
   • 特点：保证元素有序存储和快速检索
3. Linux内核
   • 场景：进程调度、内存管理的数据结构
   • 原因：在高并发环境下表现稳定
4. 数据库系统
   • 场景：某些数据库的索引结构
   • 优势：适合频繁更新的数据库环境
5. 文件系统
   • 场景：某些文件系统的目录结构
   • 特点：支持高效的目录遍历和文件查找

红黑树 vs AVL树⚔️

特性对比	红黑树	AVL树
平衡标准	颜色约束，近似平衡	高度平衡，严格平衡
旋转频率	较低，插入最多2次旋转	较高，可能频繁旋转
查询性能	良好，O(log n) ~ 2O(log n)	优秀，O(log n)
插入删除	更优，维护成本低	相对较差，维护成本高
内存开销	每个节点1bit颜色信息	每个节点存储高度(通常4字节)
适用场景	综合性能要求高的场景	查询密集型场景

建议

1. 选择时机
   • 选择红黑树：频繁插入删除，对搜索性能要求不是极致
   • 选择AVL树：搜索密集型应用，需要最优搜索性能

2.6B-树

• 概念与特征：B树（B-Tree）是一种自平衡的多路搜索树，专门为磁盘存储系统设计。它通过保持树的高度较低来最小化磁盘I/O次数，是数据库和文件系统的核心数据结构。

磁盘中读取的数据结构为什么选择B-树

• 众所周知，磁盘的读取(查找)速度很慢，那么我们就只能让读取速度为O(1)次且不存在极端情况才行

• AVL树/红黑树：O(logN)

• 哈希表：O(1) -- 但是在极端情况下哈希冲突十分严重，导致效率变为O(N)

• B-树：

  • 思想：因为红黑树/AVL树的O(logN)在上亿个数据时只要读取几十次了，那么将红黑树/AVL树压缩至一定高度(单层存更多)，那么就能提高效率
  • 在AVL搜索树的基础上找优化空间：
    1. 压缩高度，二叉变多叉
    2. 一个节点里面有多个关键字及映射的值

结构

1. 每个节点多开一个空间储存关键字

2. 新插入的节点，一定是在叶子端插入，叶子没有孩子，不会存在孩子和关键字的关系而导致混乱

3. 叶子节点的关键字满了就分裂出一个兄弟，提取中位数，向父亲插入该中位数和一个孩子

4. 满了就分裂，天然平衡，向右和向上生长

5. 只有根节点分裂才会增加一层

性质

1. 第一次分裂后，根节点至少有两个孩子

2. 每个分支节点都包含k-1个关键字和k个孩子【分支节点中孩子个数永远比关键字多一个】，其中ceil(m / 2) <= k <= m[ceil是向上取整函数]（就是说一个分支节点至少key要是半满的）

3. 每个叶子节点都包含k-1个关键字，其中ceil(m / 2) <= k <= m

4. 所有叶子节点都在同一层【完全平衡】

5. 每个节点的关键字从小到大排序，节点当中k-1个元素正好是k个孩子包含的元素的值域划分

6. 每个节点的结构为：(n，A0，K1，A1，K2，A2，…，Kn，An)其中，Ki(1 <= i <= n)为关键字，且Ki < Ki+1(1 ≤ i ≤ n-1)。Ai(0 <= i <= n)为指向子树根结点的指针。且Ai所指子树所有结点中的关键字均小于Ki+1。n为结点中关键字的个数，满足ceil(m/2) - 1 <= n <= m - 1

核心代码⚙️

#pragma once
#include <iostream>
using namespace std;

// K:关键字(B树只处理关键字); M:B树的阶数,表示B树一层有多少个节点,每个节点储存关键字的范围
template<class K, size_t M>
struct BTreeNode
{
    // 为了方便插入后再分裂,选择多给一个空间(0位置也储存数据)

    K _keys[M]; // 储存关键字的集合(M - 1个关键字)
    BTreeNode<K, M>* _subs[M + 1]; // 储存子节点指针的集合(M个子节点)
    BTreeNode<K, M>* _parent; // 双向指针之父节点指针
    size_t _num; // 实际储存了多少个关键字(_num个关键字,_num+1个节点)

    BTreeNode()
    {
        for (size_t i = 0; i < M; ++i)
        {
            _subs[i] = nullptr;
            _keys[i] = K();
        }

        _subs[M] = nullptr;
        _parent = nullptr;
        _num = 0;
    }
};

// K:磁盘地址关键字
template<class K, size_t M>
class BTree
{
    typedef BTreeNode<K, M> Node;
public:
    BTree()
        : _root(nullptr)
    {

    }

    pair<Node*, int> Find(const K& key)
    {
        // 查找的逻辑: 设置一个索引,让一个节点指针不断地将自己的_keys[index]与传入的key对比,如果比key小,说明key在该节点的左子树上,直接跳出索引查找
        // 如果比key大,说明索引还要往后走,不断与key比较,直到index = _num或者重复第一种情况,如果找到key对应的位置就直接返回

        Node* parent = nullptr; // 设置一个parent节点用于记录要找节点的上一个节点,方便后续的插入操作
        Node* cur = _root;
        while (cur) 
        {
            int index = 0;
            // 在cur对应的层中查找关键字
            while (index < cur->_num)
            {
                if (key < cur->_keys[index])
                {
                    break; // 先跳出循环,之后让cur往它的左子孩子跳入
                }
                else if (key > cur->_keys[index])
                {
                    ++index; // 往后走,直到index = _num或者key为较小者
                }
                else
                {
                    return make_pair(cur, index);
                }
            }
            // 查找完毕,在cur对应层中不存在对应关键字,往下层步入
            parent = cur;
            cur = cur->_subs[index];
        }
        // 如果查找完了发现key不存在,将parent返回,方便插入,并返回存在码-1
        return make_pair(parent, -1);
    }

    void InOrder()
    {
        _InOrder(_root);
    }

    bool Insert(const K& key)
    {
        // 插入规则:关键字只能插入到对应key位置的最低层节点上,如果该分支节点满了,就需要分裂

        // 情况1:_root为空节点
        if (_root  nullptr)
        {
            _root = new Node;
            _root->_keys[0] = key;
            ++_root->_num;

            return true;
        }

        pair<Node*, int> ret = Find(key);
        // 情况2:key已存在
        if (ret.second >= 0)
        {
            return false;
        }

        // Find函数没找到,那么返回值就是key应该插入的节点位置(因为parent节点没有左子树)
        Node* parent = ret.first; 
        Node* child = nullptr; // 第一次插入,key位置的左孩子一定空
        K newKey = key;

        while (1)
        {
            // parent作为插入位置所在的节点;newKey作为每次插入时要插入的关键字;child作为插入关键字的新的左子树子节点
            InsertKey(parent, child, newKey);
            // 1.如果节点的容量足够,直接返回
            if (parent->_num < M)
            {
                return true;
            }

            // 2.如果节点满了,那么就分裂
            // (1).创建parent的兄弟节点uncle,将parent一半的key与子节点迁移到uncle中
            #pragma region 迁移
            Node* uncle = new Node;
            size_t mid = M / 2;
            size_t j = 0;
            size_t i = mid + 1;
            for (; i < M; ++i, ++j)
            {
                uncle->_keys[j] = parent->_keys[i];
                uncle->_subs[j] = parent->_subs[i];
                // 非空连接父节点
                if (uncle->_subs[j])
                {
                    uncle->_subs[j]->_parent = uncle;
                }

                // 将迁移的元素置空
                parent->_keys[i] = K();
                parent->_subs[i] = nullptr;
            }

            // 将parent的最右节点也迁移到uncle节点
            uncle->_subs[j] = parent->_subs[i];
            if (uncle->_subs[j])
            {
                uncle->_subs[j]->_parent = uncle;
            }
            parent->_subs[i] = nullptr;

            uncle->_num = j;
            parent->_num -= j;
            #pragma endregion

            // (2).将parent中的midkey插入parent节点的_parent中
            newKey = parent->_keys[mid];
            parent->_keys[mid] = K();
            child = uncle; // uncle作为要插入到新parent节点位置的孩子child
            --parent->_num;

            // (3).判断parent的父节点是否为空
            if (parent->_parent)
            {
                parent = parent->_parent;
            }
            else
            {
                _root = new Node; // _root更新,创建一个新节点
                _root->_keys[0] = newKey;
                _root->_subs[0] = parent;
                _root->_subs[1] = uncle;
                _root->_num = 1;
                parent->_parent = _root;
                uncle->_parent = _root;
                return true;
            }
        }
    }

    // 将key插入对应的位置上
    void InsertKey(Node* targetN, Node* child, const K& key)
    {
        int endI = targetN->_num - 1;
        while (endI >= 0) 
        {
            // 将key与数组中第endI个key比较,如果比它小,就将endI位置的元素往后挪,然后继续往左探查
            if (targetN->_keys[endI] > key)
            {
                // TODO:这里能体现出_keys,_subs设置空间多一个的作用,不需要进行判空并直接分裂
                targetN->_keys[endI + 1] = targetN->_keys[endI]; 
                targetN->_subs[endI + 2] = targetN->_subs[endI + 1]; // 将对应key位置的右子树往右挪
                --endI;
            }
            // key比数组中第endI个key大,说明第key应该插入在第endI + 1个位置
            else
            {
                break;
            }
        }
        targetN->_keys[endI + 1] = key;
        targetN->_subs[endI + 2] = child; // 作为endI + 1位置的右孩子
        if (child)
            child->_parent = targetN;
        ++targetN->_num;
    }

    bool Delete(const K& key)
    {
        // 删除逻辑:删除时要先确定key所在的位置,如果key在叶子节点上,直接删除,然后要判断该叶子节点的key是否足够,不足够就需要进行合并操作,
        // 合并之后要再判断父节点的key是否足够,不足就重复合并操作,如果key在非叶子节点上,那么就要递归将该key移动到叶子节点上,再进行上述操作

        pair<Node*, int> ret = Find(key);
        // 情况1:关键字不存在,无法删除(包括_root为空的情况)
        if (ret.second  -1)
        {
            return false;
        }

        Node* cur = ret.first;
        Node* leftChild = ret.first->_subs[ret.second];
        Node* rightChild = ret.first->_subs[ret.second + 1];
        // 情况2:关键字存在,且在叶子节点中
        if (!leftChild && !rightChild)
        {
            DeleteKey(cur, key, ret.second);

            // 如果关键字个数不足
            if (cur->_num < (M + 1) / 2 - 1)
            {
                NumberLackFix(cur, cur->_parent);
            }
            return true; // 处理完毕或者关键字子树足够
        }
        // 情况3:关键字存在,但是在分支节点中,将其转化为关键字在叶子节点的情况(一个分支节点必然有左节点和右节点)
        else if(leftChild && rightChild)
        {
            // 进行递归操作,将分支节点中要删除的关键字不断与它的子节点交换直至将要删除的关键字交换到叶子节点上删除为止
            int replaceIndex;
            // 选出左右树中元素个数较多的那个
            if (leftChild->_num >= rightChild->_num)
            {
                replaceIndex = leftChild->_num - 1;
                swap(leftChild->_keys[replaceIndex], cur->_keys[ret.second]);
                return DeleteRecursive(leftChild, replaceIndex);
            }
            else
            {
                replaceIndex = 0;
                swap(rightChild->_keys[replaceIndex], cur->_keys[ret.second]);
                return DeleteRecursive(rightChild, replaceIndex);
            }
        }
    }

private:
    Node* _root;

    void _InOrder(Node* node)
    {
        if (node  nullptr)
        {
            return;
        }

        for (size_t i = 0; i < node->_num; ++i)
        {
            // 从左节点依次往右遍历
            _InOrder(node->_subs[i]);
            cout << node->_keys[i] << " "; // 输出_num个关键字
        }
        _InOrder(node->_subs[node->_num]); // 最后的右节点
    }

    // 递归删除逻辑,查看该节点的子节点是否为空,从而决定是否要继续递归下去
    bool DeleteRecursive(Node* node, int index)
    {
        Node* leftChild = node->_subs[index];
        Node* rightChild = node->_subs[index + 1];

        // 情况2:关键字存在,且在叶子节点中
        if (!leftChild && !rightChild)
        {
            DeleteKey(node, node->_keys[index], index);

            // 如果关键字个数不足
            if (node->_num < (M + 1) / 2 - 1)
            {
                NumberLackFix(node, node->_parent);
            }
            return true; // 处理完毕或者关键字子树足够
        }
        else
        {
            // 进行递归操作,将分支节点中要删除的关键字不断与它的子节点交换直至将要删除的关键字交换到叶子节点上删除为止
            int replaceIndex;
            // 选出左右树中元素个数较多的那个
            if (leftChild->_num >= rightChild->_num)
            {
                replaceIndex = leftChild->_num - 1;
                swap(leftChild->_keys[replaceIndex], node->_keys[index]);
                return DeleteRecursive(leftChild, replaceIndex);
            }
            else
            {
                replaceIndex = 0;
                swap(rightChild->_keys[replaceIndex], node->_keys[index]);
                return DeleteRecursive(rightChild, replaceIndex);
            }
        }
    }

    void DeleteKey(Node* target, const K& key, const int& index)
    {
        int pos = index + 1;
        while (pos < target->_num)
        {
            target->_keys[pos - 1] = target->_keys[pos];
            ++pos;
        }

        --target->_num;
    }

    void NumberLackFix(Node* target, Node* targetParent)
    {
        // 说明target节点即是根节点,也是叶子节点,所以key的个数可以任意,直接返回即可
        if (target  nullptr)
        {
            return;
        }

        // 找target节点对应为parent的第几个节点
        int pos = 0;
        for (; pos <= targetParent->_num; ++pos)
        {
            if (targetParent->_subs[pos]  target)
            {
                break;
            }
        }

        // 左右兄弟节点
        Node* left = pos  0 ? nullptr : targetParent->_subs[pos - 1];
        Node* right = pos  targetParent->_num ? nullptr : targetParent->_subs[pos + 1];

        // 向左兄弟借关键字
        if (left && left->_num > (M + 1) / 2)
        {
            // 将父节点pos位置的key下沉到target中,然后将左兄弟的最大关键字上移到parent中(右单旋)
            for (int i = 0; i < target->_num; ++i)
            {
                target->_keys[i + 1] = target->_keys[i];
            }
            target->_keys[0] = targetParent->_keys[pos];
            targetParent->_keys[pos] = left->_keys[left->_num - 1];
            --left->_num;
            ++target->_num;
        }
        // 向右兄弟借关键字
        else if (right && right->_num > (M + 1) / 2)
        {
            // 将父节点pos位置的key下沉到target中,然后将右兄弟的最小关键字移到parent中(左单旋)
            target->_keys[target->_num - 1] = targetParent->_keys[pos];
            targetParent->_keys[pos] = right->_keys[0];
            for (int i = 1; i < right->_num; ++i)
            {
                right->_keys[i - 1] = right->_keys[i];
            }
            --right->_num;
            ++target->_num;
        }
        // 左右兄弟都没有富余,将该节点与兄弟节点合并
        else
        {
            Node* newTarget = targetParent;
            // TODO:考虑左右有节点不存在的情况
            if (left)
            {
                Integrate(target, left, pos);
            }
            else if(right)
            {
                Integrate(right, target, pos + 1);
            }
            // 如果合并后,父节点的key不够,才继续向上调整
            if(newTarget && newTarget->_num < (M + 1) / 2 - 1)
                NumberLackFix(newTarget, newTarget->_parent);
        }
    }

    void Integrate(Node* self, Node* leftBro, int index)
    {
        // 先将index位置的key移动到leftBro,然后将自己的节点全部转移到leftBro的后面
        Node* parent = self->_parent;
        K key = parent->_keys[index - 1]; // 在left和self之间的位置

        // 将parent的_keys与_subs进行更新
        int pos = index;
        while (pos < parent->_num)
        {
            parent->_keys[pos - 1] = parent->_keys[pos];
            parent->_subs[pos] = parent->_subs[pos + 1];
            ++pos;
        }
        --parent->_num;

        // 将key插入到leftBro中
        leftBro->_keys[leftBro->_num] = key;
        ++leftBro->_num;
        // 开始将self中的数据迁移到leftBro中
        int counter = self->_num;
        int i = leftBro->_num;
        int j = 0;
        while (counter > 0)
        {
            leftBro->_keys[i] = self->_keys[j];
            leftBro->_subs[i] = self->_subs[j];
            if (self->_subs[j])
                self->_subs[j]->_parent = leftBro;
            ++i, ++j, --counter;
        }
        leftBro->_subs[i] = self->_subs[j]; // self的最右子节点也迁移到leftBro中
        if (self->_subs[j])
            self->_subs[j]->_parent = leftBro;
        leftBro->_num += self->_num;
        delete self;
        parent->_subs[index] = nullptr;

        // 考虑parent为_root的情况
        if (parent->_parent  nullptr && parent->_num  0) 
        {
            _root = leftBro; // 将插入的"左孩子"位置是为新的root节点
            _root->_parent = nullptr;
            delete parent;
        }
    }
};

总结：B树的优势与应用💡

优势	说明
磁盘友好	节点大小匹配磁盘页，减少I/O
高度平衡	所有操作保持O(log n)复杂度
范围查询	天然支持高效的范围扫描
大规模数据	适合存储海量数据

• 适用场景

1. 数据库管理系统
   • 索引结构
   • 数据存储
2. 文件系统
   • 目录管理
   • 元数据存储
3. 大数据存储
   • 键值数据库
   • 分布式存储

Part3：其他结构

3.1哈希表🔑➡️📊

• 出现的背景：想找一种理想的方法，使其可以不经过任何比较，一次直接从表中得到要搜索的元素，如果构造一种存储结构，通过某种函数（hashFunc）使元素的存储位置和它的关键码之间能够建立起一一映射的关系，那么在查找时通过该元素可以很快找到该元素。
• 概念与特征：哈希表（Hash Table）是一种通过哈希函数将键映射到表中特定位置来进行数据访问的数据结构，提供近乎常数时间的查找性能

哈希表的核心规则

哈希函数

• 因为哈希的本质其实是一种映射的对应关系，为了达成想要的映射关系，我们必须找到一种方式来构建一个哈希函数来进行映射操作

• 常见的哈希函数构造方式：

  1. 直接定址法：映射只跟关键字直接或者间接(如数据间的相对位置)相关【问题是当数据太过离散时效率很低，空间消耗大】
  2. 除留余数法：key % 表大小的余数是多少，就把这个数据放在哪个位置【问题时无法存储位置相同的数据，两个数据会存在一个空间中，导致哈希冲突，降低效率】

冲突

• 定义：不同的值映射到了相同的位置【使哈希表效率降低的最大问题】

• 冲突的解决方案：

  1. 闭散列——开放定址法：当发生哈希冲突时，若哈希表未被装满，说明哈希表中必然有空位，那么可以把数据存放到冲突位置的"下一个"空位上。【问题：如果冲突的越厉害，那么效率越低，适合冲突少的情况】

     • 如何寻找冲突位置的"下一个"位置？ 使用探测：

     1. 线性探测：依次往后找一个空位置

        • 缺点：线性探测的思路就是我的位置被占据了，所以就挨着往后直接占用别人的位置，可能导致一片一片的冲突【洪水效用】

     2. 二次探测：依2次方的速度往后找一个空位置【如1^2^，2^2^，3^2^，...】

        • 对比线性探测：让冲突的数据分布的更分散，不容易集聚在一起导致连片的冲突

     • 如何解决查找时的遇见被删除位置直接退出的问题：设置状态来决定是否继续查找，状态分为三种

     • empty：空（不会进行查找）

     • exist：存在（会查找）

     • delete：删除（会查找）

     • 缺点：扩容时需要消耗比较多的资源，且因为会影响数组的长度，所以需要进行重新映射的操作，很消耗资源，总体来说不是一个好的解决方法，因为它是一种抢占式的思路，哈希冲突会互相影响，导致总体的效率很低

  2. 开散列——链地址法【哈希桶】：首先对关键码集合用散列函数计算散列地址，具有相同地址的关键码(映射地址相同)归于同一子集合，每个子集合称为一个桶，各个桶中的元素通过一个单链表连接起来，各链表的头节点储存在哈希表中。

     • 结构图：

     

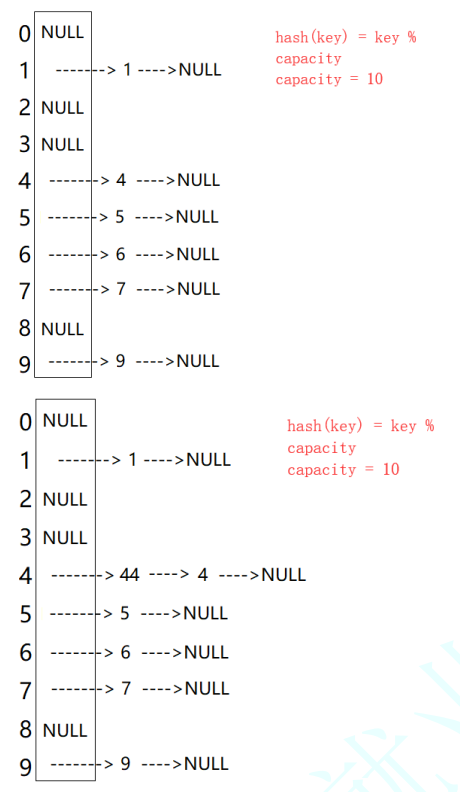
     • 注意事项⚠️：当大量的数据冲突，这些哈希冲突的数据就会挂在同一个链式桶中，导致查找效率降低，所以开散列也需要控制哈希冲突的，通过限制控制负载因子，不过这里就可以把空间利用率提高一些，负载因子也可以高一些，一般把开散列的负载因子控制到1会好一些
     • 负载因子 = 表中数据 / 表的大小 【衡量哈希表满的程度，负载因子越大，哈希表的效率越低（冲突一般越多了）】

核心代码⚙️

#pragma once
#include <iostream>
#include <string.h>
#include <vector>
using namespace std;

// 用于做测试的KOfT
template<class K>
struct SetKeyOfT
{
    const K& operator()(const K& key)
    {
        return key;
    }
};

// 闭散列
namespace CLOSE_HASH
{
    // 状态,记录每个位置的节点状态,决定了数据是否存在
    enum State
    {
        Empty, // 1
        Exist, // 2
        Delete, // 3
    };

    // 每个节点位置存储的数据
    template<class T>
    struct HashData
    {
        T _data;
        State _state;
    };

    template<class K, class T, class KOfT>
    class HashTable
    {
        typedef HashData<T> HashData;
    public:
        HashTable()
        {
            _table.resize(10); // 初始化一个默认容量
        }

        bool Insert(const T& data)
        {
            KOfT koft;
            size_t tableSize = _table.size();
            // 检查vector的size是否正常初始化,并检查负载因子
            if (tableSize  0 || _num * 10 / tableSize >= 7)
            {
                #pragma region 注释
                // 正常方式: 开新表,将旧数据映射到新表中,之后进行swap操作
                //vector<HashData> newTable;
                //size_t newSize = tableSize  0 ? 10 : tableSize * 2;
                //newTable.resize(newSize);

                //for (int i = 0; i < tableSize; ++i)
                //{
                //  // 如果数据存在,进行拷贝
                //  if (_table[i]._state  Exist)
                //  {
                //      size_t index = i;
                //      // 检查数据是否发生了连续的哈希冲突
                //      while (newTable[i]._state  Exist)
                //      {
                //          index = (index + 1) % newSize; // 取余,防止超出作用域
                //      }
                //  }
                //  newTable[index] = _table[i]; // 将数据和状态复制过去
                //}
                //// 两者交换地址
                //_table.swap(newTable);
                #pragma endregion

                // 高效映射(因为后面也要进行寻址操作,所以使用递归能够减少重复代码的编写)
                HashTable<K, T, KOfT> newTable;
                size_t newSize = tableSize  0 ? 10 : tableSize * 2;
                newTable._table.resize(newSize);

                for (int i = 0; i < tableSize; ++i)
                {
                    // 如果数据存在,就拷贝进新哈希表中
                    if (_table[i]._state  Exist)
                    {
                        newTable.Insert(_table[i]._data);
                    }
                }
                _table.swap(newTable._table); // 交换两者的_table数据即可
            }

            // 如果size和负载因子正常,进行插入操作
            // 二次探测
            tableSize = _table.size();
            size_t pos = koft(data) % tableSize; // 起始位置
            size_t index = pos;
            size_t times = 1; // 次数

            // 如果数据存在,就开始探测
            while (_table[index]._state  Exist)
            {
                // TODO:注意,因为是插入键值对数据,所以键不能重复
                if (koft(data)  koft(_table[index]._data))
                    return false;

                index = (index + times * times) % tableSize;
                ++times;
            }
            _table[index]._data = data;
            _table[index]._state = Exist;
            ++_num;

            return true;
        }

        HashData* Find(const K& key)
        {
            // 通过_table的size查看_table是否为空
            if (_table.empty())
                return nullptr;

            KOfT koft;
            size_t index = key % _table.size();
            // TODO:因为前面插入使用的是二次探测,所以查找使用的也要是二次探测
            size_t times = 1;
            // 进行查找,但是index对应的节点存在不能说明对应键位置的值就存在,因为可能存在哈希冲突,需要排查
            while (_table[index]._state != Empty)
            {
                if (koft(_table[index]._data)  key)
                {
                    if (_table[index]._state  Exist)
                        return &_table[index];
                    else
                        return nullptr; // 改键对应位置的数据已被删除
                }
                index = (index + times * times) % _table.size();
                ++times;
            }

            return nullptr;
        }

        bool Erase(const K& key)
        {
            if (_table.empty())
                return false;
            HashData* del = Find(key);
            // 如果key存在,进入下面的逻辑
            if (del)
            {
                del->_state = Delete;
                return true;
            }
            return false;
        }
    private:
        vector<HashData> _table;
        size_t _num = 0; // 设置一个变量num原来表示存储了多少个数据,计算负载因子要使用
    };
}

// 开散列
namespace OPEN_HASH
{
    template<class T>
    struct __HashNode
    {
        // 类的构造函数不需要写泛型
        __HashNode(const T& data)
            : _data(data)
            , _next(nullptr)
        {

        }

        T _data;
        __HashNode<T>* _next;
    };

    // 前置声明
    template<class K, class T, class KOfT, class Hash>
    class HashTable;

    template<class K, class T, class KOfT, class Hash>
    struct __HashTableIterator
    {
        typedef __HashNode<T> Node;
        typedef HashTable<K, T, KOfT, Hash> HT;
        typedef __HashTableIterator<K, T, KOfT, Hash> Self;
        // 使用指针获取HT和Node对象,使用指针比引用更加灵活
        HT* _pht;
        Node* _node;

        __HashTableIterator(HT* pht, Node* node)
            : _pht(pht)
            , _node(node)
        {

        }

        T& operator*()
        {
            return _node->_data;
        }

        T* operator->()
        {
            return &(_node->_data);
        }

        // 前++(无前--,因为forward_list不支持双向查找)
        Self& operator++()
        {
            // 看看是否已经是遍历终点
            if (_node  nullptr)
                return *this;

            KOfT koft;
            // 1.如果++后的结果不为nullptr,那么直接返回
            // 2.结果为nullptr,就在哈希表上往后找
            if (_node->_next != nullptr)
            {
                _node = _node->_next;
                return *this;
            }
            else
            {
                // 获取_node对应_data的键位置的下一个位置
                size_t index = _pht->HashFunc(koft(_node->_data)) % _pht->_table.size() + 1;
                // 找下一个不为空的哈希表元素
                for (; index < _pht->_table.size(); ++index)
                {
                    if (_pht->_table[index] != nullptr)
                    {
                        _node = _pht->_table[index];
                        return *this;
                    }
                }

                // 如果找完了还为nullptr,就返回nullptr,表示遍历完成
                _node = nullptr;
                return *this;
            }
        }

        bool operator!=(const Self& s)
        {
            return s._node != _node; // 通过比较_node地址或者指向的_data数据
        }

        bool operator(const Self& s)
        {
            return s._node  _node;
        }
    };

    // 泛用类型的Hash函数
    template<class K>
    struct Hash
    {
        const K& operator()(const K& key)
        {
            return key;
        }
    };

    template<>
    struct Hash<string>
    {
        size_t operator()(const string& key)
        {
            // BKDR Hash方法
            size_t hash = 0;
            for (size_t i = 0; i < key.length(); i++)
            {
                hash *= 131;
                hash += key[i];
            }
            return hash;
        }
    };

    template<class K, class T, class KOfT, class Hash = Hash<K>>
    class HashTable
    {
        typedef __HashNode<T> Node; // 内部成员,写在private域中
    public:
        friend __HashTableIterator<K, T, KOfT, Hash>; // 友元,单方面允许迭代器调用HashTable的私有,保护成员
        typedef __HashTableIterator<K, T, KOfT, Hash> iterator; // 外部调用的工具,写在public域中

        // TODO:将各种数据类型转换为索引值的函数
        size_t HashFunc(const K& key)
        {
            Hash hash;
            return hash(key);
        }

        iterator begin()
        {
            // 找第一个存在的节点
            for (int i = 0; i < _table.size(); ++i)
            {
                if (_table[i] != nullptr)
                {
                    return iterator(this, _table[i]);
                }
            }

            return end();
        }

        iterator end()
        {
            return iterator(this, nullptr);
        }

        ~HashTable()
        {
            Clear();
        }

        // 清除哈希表的每个哈希桶需要手动解决
        void Clear()
        {
            for (int i = 0; i < _table.size(); ++i)
            {
                Node* cur = _table[i];
                while (cur)
                {
                    Node* next = cur->_next;
                    delete cur;
                    cur = next;
                }
                // 置空,防止野指针
                _table[i] = nullptr; 
            }
        }

        pair<iterator, bool> Insert(const T& data)
        {
            KOfT koft;
            size_t tableSize = _table.size();
            // 检查负载因子
            if (tableSize  0 || _num  tableSize)
            {
                vector<Node*> newT;
                size_t newSize = tableSize  0 ? 10 : tableSize * 2;
                newT.resize(newSize);
                // 重新映射
                for (int i = 0; i < tableSize; ++i)
                {
                    Node* cur = _table[i];
                    // 表中的每个数据都要重新映射,因为之前在一个桶上的数据重新映射的位置可能会不同
                    while (cur)
                    {
                        Node* next = cur->_next;
                        size_t index = HashFunc(koft(cur->_data)) % newSize;

                        // 头插
                        cur->_next = newT[index]; // 将newT[index]位置的链桶挂在新插入的节点后面
                        newT[index] = cur; // 然后将新插入的节点当作新的new[index]头节点

                        cur = next;
                    }
                    // 置空,防止析构时将newT中的空间释放
                    _table[i] = nullptr;
                }
                _table.swap(newT);
            }

            // 插入
            tableSize = _table.size(); // 重新获取一下长度
            size_t index = HashFunc(koft(data)) % tableSize;
            Node* cur = _table[index];
            while (cur)
            {
                // 如果是string类型,也会使用strcmp,直接用koft即可
                if (koft(data)  koft(cur->_data))
                {
                    // 键相同
                    return make_pair(iterator(this, cur), false);
                }
                else
                {
                    cur = cur->_next;
                }
            }

            // 头插(如果没有键相同的情况就到这里)
            Node* newNode = new Node(data);
            newNode->_next = _table[index];
            _table[index] = newNode;

            ++_num;
            return make_pair(iterator(this, newNode), true);
        }

        iterator Find(const K& key)
        {
            KOfT koft;
            size_t index = HashFunc(key) % _table.size();
            Node* cur = _table[index];
            while (cur)
            {
                if (koft(cur->_data)  key)
                {
                    return iterator(this ,cur);
                }
                cur = cur->_next;
            }

            return iterator(this, nullptr);
        }

        bool Erase(const K& key)
        {
            KOfT koft;
            size_t index = HashFunc(key) % _table.size();
            Node* cur = _table[index]; // 因为需要找到前置指针,所以不能用Find直接返回一个Node 
            Node* prev = nullptr;
            while (cur)
            {
                if (koft(cur->_data)  key)
                {
                    if (prev)
                    {
                        prev->_next = cur->_next;
                    }
                    else
                    {
                        _table[index] = cur->_next;
                    }
                    // 删除
                    delete cur;
                    return true; 
                }
                prev = cur;
                cur = cur->_next;
            }

            return false;
        }
    private:
        vector<Node*> _table;
        size_t _num = 0;
    };
}

操作性能分析📈

操作	函数	时间复杂度	说明
✅ 增	Insert	平均O(1)，最坏O(n)	依赖负载因子和哈希函数质量
❌ 删	Erase	平均O(1)，最坏O(n)	分离链接法直接删除，开放定址法标记删除
🔍 查	Find	平均O(1)，最坏O(n)	理想情况下常数时间访问

unordered_set与unordered_map

• Cpp中的unordered_set与unordered_map是通过哈希表来实现的，下面是unordered_set与unordered_map的模拟代码

#include "Hash.h"

// 防止与标准库中的数据结构冲突
namespace MyUnorderedMap
{
    template<class K, class V, class Hash = OPEN_HASH::Hash<K>>
    class unordered_map
    {
        struct MapKOfT
        {
            const K& operator()(const pair<K, V>& kv)
            {
                return kv.first;
            }
        };

    public:
        typedef typename OPEN_HASH::HashTable<K, pair<K, V>, MapKOfT, Hash>::iterator iterator;
        iterator begin()
        {
            return _hashTable.begin();
        }

        iterator end()
        {
            return _hashTable.end();
        }

        pair<iterator, bool> Insert(const pair<K, V>& kv)
        {
            return _hashTable.Insert(kv);
        }

        iterator Find(const K& key)
        {
            return _hashTable.Find(key);
        }

        // 返回值的引用
        V& operator[](const K& key)
        {
            pair<iterator, bool> ret = _hashTable.Insert(make_pair(key, V())); // 如果值存在,返回对应位置的键值对,否则就创建一个新的键值对
            return ret.first->second;
        }
    private:
        OPEN_HASH::HashTable<K, pair<K, V>, MapKOfT, Hash> _hashTable;
    };
}

// 防止与标准库中的数据结构冲突
namespace MyUnorderedSet
{
    template<class K, class Hash = OPEN_HASH::Hash<K>>
    class unordered_set
    {
        struct SetKOfT
        {
            const K& operator()(const K& k)
            {
                return k;
            }
        };

    public:
        typedef typename OPEN_HASH::HashTable<K, K, SetKOfT, Hash>::iterator iterator;
        iterator begin()
        {
            return _hashTable.begin();
        }

        iterator end()
        {
            return _hashTable.end();
        }

        pair<iterator, bool> Insert(const K& key)
        {
            return _hashTable.Insert(key);
        }

        iterator Find(const K& key)
        {
            return _hashTable.Find(key);
        }
    private:
        OPEN_HASH::HashTable<K, K, SetKOfT, Hash> _hashTable;
    };
}

• 测试样例：

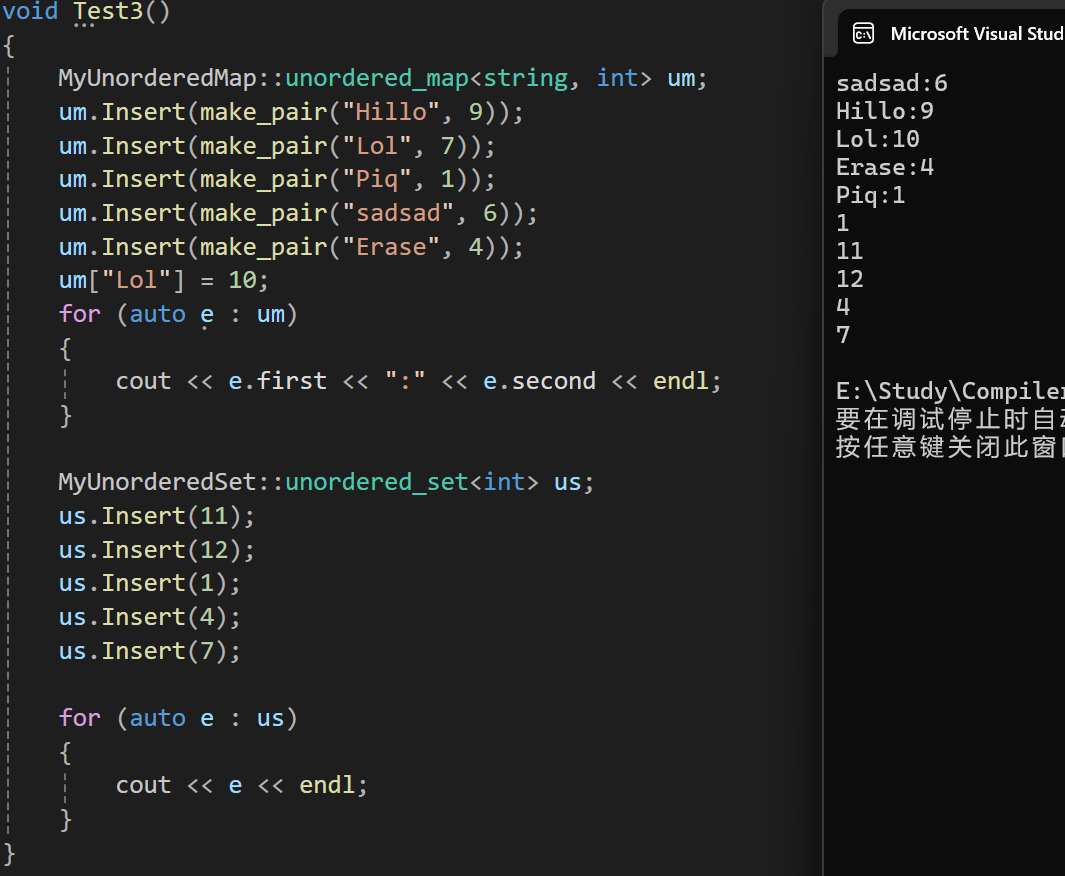
总结：哈希表的优势与应用💡

优势	说明
极致性能	平均情况下O(1)时间复杂度的查找、插入、删除
灵活键类型	支持任意可哈希类型作为键
动态调整	自动扩容维持性能，适应数据量变化
空间效率	相比树结构，通常有更好的空间利用率

• 实际应用场景

1. 编程语言内置数据结构
   • 场景：Python的dict、Java的HashMap、C++的unordered_map
   • 优势：作为语言核心数据结构，提供快速键值访问
2. 数据库索引
   • 场景：哈希索引、内存数据库
   • 特点：适合等值查询，不适合范围查询
3. 缓存系统
   • 场景：Redis、Memcached等内存缓存
   • 需求：需要极快的键值查找速度
4. 编译器实现
   • 场景：符号表、字符串池
   • 优势：快速的名字查找和解析
5. 网络安全
   • 场景：密码哈希、数字签名
   • 应用：MD5、SHA系列哈希算法
6. 分布式系统
   • 场景：一致性哈希、负载均衡
   • 特点：在分布式环境中提供数据定位

与平衡树结构对比⚖️

特性	哈希表	红黑树/AVL树
平均性能	O(1)，极致快速	O(log n)，稳定但稍慢
最坏性能	O(n)，可能退化	O(log n)，保证稳定
有序性	不保持元素顺序	保持元素有序
内存使用	通常更节省	需要额外平衡信息
适用查询	等值查询	范围查询、有序遍历

3.1(1)位图

• 介绍：位图是哈希的一种特殊应用，旨在处理存储大量整型数据时提高效率

• 核心：有时候我们会遇见让你在大量数据中查找一个数据是否存在，此时如果还是使用int储存单个数据，那么将会导致空间不够的情况，此时就需要将储存单位换为位，1个int等效为32个位，这样就能使储存空间大大减少【即节省空间，效率又非常高】

核心代码⚙️

#pragma once
#include <iostream>
#include <string.h>
#include <vector>
using namespace std;

// 位图是一种通过映射关系将数据储存在比特位中的数据结构(只适合储存整型)
namespace MyBitSet
{
    class bitset
    {
    public:
        // 要开多少个位的空间(向上取整)
        bitset(size_t N)
        {
            _bitset.resize(N / 32 + 1);
            _num = 0;
        }

        // 标志位(相当于插入)
        void set(size_t x)
        {
            size_t space = x / 32; // 插入的数组空间
            size_t pos = x % 32; // 插入数组空间中的位置
            // 将第space个数组上的index位上的值赋值为1
            // 0或上任意数A,结果都为A,利用这个特性,我们让1向高位移动pos位,TODO:那么0或上(1 << pos)的结果就是在目标位置的数码为1
            _bitset[space] |= (1 << pos);
            ++_num;
        }

        // 重新标志位(相当于删除)
        void reset(size_t x)
        {
            size_t space = x / 32;
            size_t pos = x % 32;
            // 将(1 << pos)取反,然后按位与,就能将目标位的1变为0,而除目标位外的所有1能保持不变
            _bitset[space] &= ~(1 << pos); 
        }

        // 判断数据x是否存在
        bool test(size_t x)
        {
            size_t space = x / 32;
            size_t pos = x % 32;
            // 直接在目标位按位与1,如果目标位为1,返回1,目标位为0,返回0
            return _bitset[space] & (1 << pos);
        }
    private:
        std::vector<int> _bitset;
        size_t _num; // 储存了多少个元素
    };
}

• 位图的应用：

  1. 快速查找某个数据是否在一个集合中

  2. 排序 + 去重

  3. 求两个集合的交集，并集等

  4. 操作系统中的磁盘块标记

总结：位图的优势与应用💡

优势	说明
极致空间效率	每个元素仅需1比特位，比传统数据结构节省32倍空间
超高操作速度	O(1)时间复杂度的查找、设置、清除操作
缓存友好	连续内存布局，充分利用CPU缓存

• 缺点：不过位图有个很大的缺点，那就是只能处理整型数据

• 实际应用场景

  1. 大数据去重
     • 场景：URL去重、用户ID去重
     • 优势：使用少量内存处理海量数据去重
     • 示例：使用1GB内存可处理80亿条数据去重
  2. 布隆过滤器
     • 场景：缓存穿透保护、爬虫URL判重
     • 特点：空间效率极高，存在一定误判率
     • 应用：Redis、数据库查询优化

3.2并查集

• 概念与特征：并查集（Union-Find/Disjoint Set）是一种用于处理不相交集合合并与查询问题的树型数据结构。它支持高效的合并操作和查找操作，是解决连通性问题的核心工具，也是实现图所必要的前置数据结构
• 本质：并查集本质上是一个森林(多颗树组成的结构)

结构

1. 像堆类似用数组表示多颗树【下标表示关系，开始每个位置都是-1，表示每个元素都是一个集合】
2. 使用了双亲表示法【当两个节点建立关系时，父亲位置存的值加上孩子位置存的值，然后孩子位置存父亲位置的下标->如果下标位置的值为负数则说明这个节点是树的根节点，否则是子节点，子节点位置的值指向根节点的位置】
3. 集合的再次合并：将并入节点位置的值加到新根节点中【所以子节点越多，根位置的值越小，根节点位置的值表示的是该树的节点个数】

• 路径压缩：当子节点的父节点不是集合的根节点时，把子节点移动到根节点的子节点位置即可【当并查集的数据量很大时，就需要使用路径压缩来提高效率了，一般是在FindRoot函数中进行路径压缩(边找边压缩)】

核心代码⚙️

#pragma once
#include <iostream>
#include <vector>
using namespace std;

// 构造一个最基础的并查集
// 什么是并查集:并查集实际上是一个森林,可以储存多个集合,能够对集合进行合并和查询
// 并查集的结构特征:并查集是一个数组,每个索引都是一个元素,数组每个位置储存的值是该元素的根节点位置(指向对应索引位置)
class DisjiontSet
{
public:
    DisjiontSet(size_t n)
        : _DjSet(n, -1) // 创建并查集,手动给予长度,将每个元素的值改为-1(说明他们自身作为自己的根节点TODO:[开始时,每个元素都是一个集合])
    {

    }

    // 合并
    void Union(int x1, int x2)
    {
        if (x1 < 0 || x2 < 0 || x1 >= _DjSet.size() || x2 >= _DjSet.size())
        {
            throw "异常数据输入";
            return;
        }

        // 在合并的时候可以顺便路径压缩
        int root1 = FindRoot(x1);
        int root2 = FindRoot(x2);
        if (root1  root2)
        {
            return;
        }

        // 合并规则:将数据量小的集合挂在数据量大的集合中(这样更少的数据层数变高)
        // _DjSet[根节点]的值越小(负数),表示,该根节点挂载的数据越多
        if (_DjSet[root1] > _DjSet[root2])
        {
            swap(root1, root2); // 将指向的_DjSet[根节点]值较小的root换到root1
        }

        // 合并并更新
        _DjSet[root1] += _DjSet[root2];
        _DjSet[root2] = root1;
    }

    // 找元素x的根节点位置
    int FindRoot(int x)
    {
        if (x >= _DjSet.size() || x < 0)
        {
            throw "异常数据输入";
            return -1;
        }

        int parent = x;
        // 如果_DjSet[n]储存的元素为负数,说明n是根节点,否则继续查找
        while (_DjSet[parent] >= 0)
        {
            parent = _DjSet[parent];
        }

        // 路径压缩(向上找根节点,并将路上的非根节点的子节点挂在根节点的子节点位置,数据量多时提高查找效率)
        while (_DjSet[x] >= 0) // 父节点为非负数时压缩路径
        {
            // 记录x当前父节点的位置
            int root = _DjSet[x];
            _DjSet[x] = parent;

            // 向上调整
            x = root;
        }

        return parent;
    }

    // 查看两个元素是否在同一个集合中(同一棵树中)
    bool InSet(int x1, int x2)
    {
        if (x1 < 0 || x2 < 0 || x1 >= _DjSet.size() || x2 >= _DjSet.size())
        {
            throw "异常数据输入";
            return false;
        }

        return FindRoot(x1)  FindRoot(x2);
    }

    // 计算一下并查集中有多少一棵树
    int TreeSize()
    {
        size_t size = 0;
        for (int i = 0; i < _DjSet.size(); ++i)
        {
            if (_DjSet[i] < 0)
            {
                ++size;
            }
        }

        return size;
    }

private:
    vector<int> _DjSet; // 不选择适用链式结构来实现,而是使用数组来实现并查集,这与并查集自身的功能有关
};

• 测试样例：

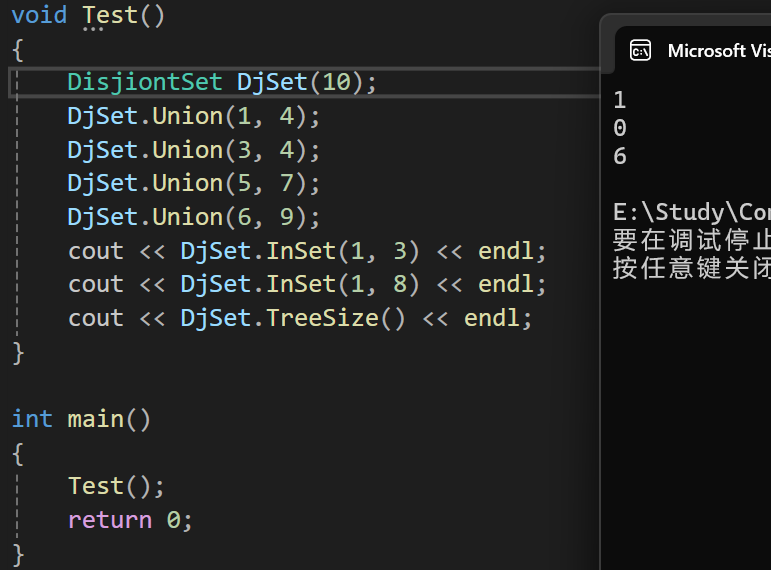
总结：并查集的优势与应用💡

优势	说明
高效动态连通性	支持快速合并和查询连通性
近似常数时间	优化后操作接近O(1)时间复杂度
空间效率	仅需O(n)空间，实现简单
算法基石	是许多高级算法的基础组件

3.3图

• 概念与特征：图（Graph）是由顶点集合及顶点间的关系组成的一种数据结构：G = (V，E)，其中顶点集合V = {X|X属于某个数据对象集}是有穷非空集合；E = {(x，y)|x，y属于V}或者E = {<x，y>|x，y属于V && Path(x，y)}是顶点关系的有穷集合，也叫边的集合【G：graph V：vertex E：edge】
  • 顶点和边：图中的节点称为顶点，两个顶点相关联构成边【<x，y>是有向边；(x，y)是无向边】

关于图的名词

• 完全图：在有n个顶点的无向图中，若是有n (n - 1) / 2条边，即任意两个顶点之间有且仅有一条边，那么这个图就是无向完全图；若在n个顶点的有向图中，有n (n - 1)条边，即任意两个顶点之间有且仅有两条方向相反的边，那么这个图就是有向完全图【跟完全二叉树的定义很像】

• 邻接顶点：在无向图中G中，若(u,v)是E(G)中的一条边，则称u和v互为邻接顶点，并称边(u, v)依附于顶点u和v；在有向图G中，若<u，v>是E(G)中的一条边，则称顶点u邻接到v，顶点v邻接自顶点u，并称边<u，v>与顶点u和顶点v相关联【有向图还是邻接方向】

• 顶点的度：顶点v的度是指与它相关联的边的条数，记作deg(v)。在有向图中，顶点的度等于该顶点的入度与出度之和，其中顶点v的入度是以v为终点的有向边的条数，记作indev(v)；顶点v的出度是以v为起始点的有向边的条数，记作outdev(v)。因此：dev(v)=indev(v)+outdev(v)。注意：对于无向图，顶点的度等于该顶点的入度和出度，即dev(v)=indev(v)=outdev(v)

• 路径：在图G = (V，E)中，若从顶点vi出发有一组边使其可到达顶点vj，则称顶点vi到顶点vj的顶点序列为从顶点vi到顶点vj的路径【即至少有间接连接就行】

• 路径长度：对于不带权的图，一条路径的路径长度是指该路径上的边的条数；对于带权的图，一条路径的路径长度是指该路径上各个边权值的总和

• 简单路径与回路：若路径上各顶点v1，v2，v3，…，vm均不重复，则称这样的路径为简单路径。若路径上第一个顶点v1和最后一个顶点vm重合，则称这样的路径为回路或环。

• 子图：设图G = {V，E}和图G1 = {V1，E1}，若V1属于V且E1属于E，则称G1是G的子图【顶点和边是原图的一部分】

• 连通图：在无向图中，若从顶点v1到顶点v2有路径，则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的，则称此图为连通图。

• 强连通图：在有向图中，若在每一对顶点vi和vj之间都存在一条从vi到vj的路径，也存在一条从vj到vi的路径，则称此图是强连通图

• 生成树：一个连通图(无向图限定)的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条边。【在最少边的情况下达成联通】

• 最小连通： 回路：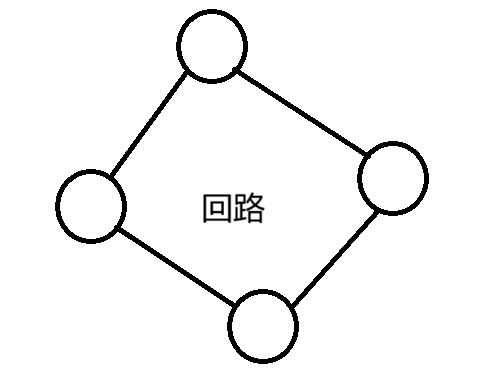

图的储存结构

邻接矩阵

• 定义：邻接矩阵是一个二维数组，先用一个数组将顶点保存，然后采用矩阵来表示节点和节点之间的关系
• 优点：
  • 非常适合存储稠密图
  • 能够O(1)地判断两个顶点的连接关系，并取到权值

• 缺点：

  • 不适合用来查找一个顶点连接的所有边，需要O(N)

​

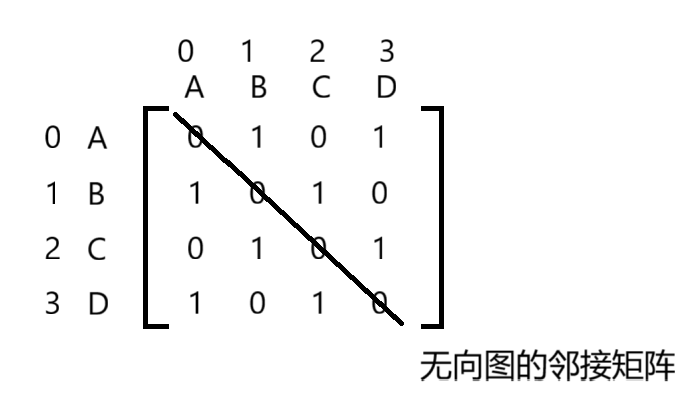
邻接表

• 定义：是一个指针数组，每个指针把自己连接的顶点都挂在自己下面【有向图一般只需要存储一个出边表(类似于"我的关注列表")即可，无特殊需要不需要存储入边表】

• 优点：

  • 适合存储稀疏图(有一个存一个)
  • 适合查找一个顶点连接出去的边

• 缺点：

  • 不适合确定两个顶点是否相连及其权值

  

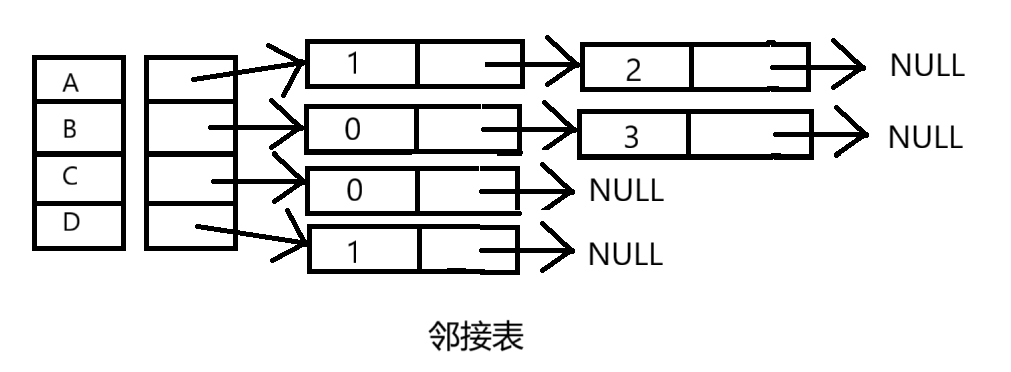
• 总结：邻接表和邻接矩阵是相辅相成的两种结构，互有优缺点

遍历

• 广度优先遍历：和二叉树一样，使用队列即可，不过因为图的结构可能导致重复，所以还需要一个标记数组来标记已经入队列的节点
• 深度优先遍历：也是和二叉树一样，采用递归调用的方式，十分简单【注：图是很容易过深的数据结构，所以到一定程度了DFS也不适合图使用】

最小生成树

• 连通图中的每一棵生成树，都是原图的一个极大无环子图，即从其中删去任何一条边，生成树就不再连通；反之，在其中引入任何一条新边，都会形成一条回路。

• 定义：构成生成树的这些边加起来的权值和是最小的生成树就是最小生成树【用最小的成本让这N个顶点连通起来】

• 构造最小生成树的三条准则：

  1. 只能使用图中权值最小的边来构成生成树
  2. 只能使用恰好n-1条边来连接图的n个顶点
  3. 选用的n-1条边不能构成回路

• 构造最小生成树的算法：

  1. Kruskal算法：用贪心算法，每次都选择权值最小的边(未选择)，如果构成了回路(使用并查集判断)，就选权值第二小的边，然后以此往复【可以通过排序获取顺序或者用优先级队列也很合适】(离散连接)
  2. Prim算法：跟Kruskal算法类似，Prim 算法所具有的一个性质是集合A中的边总是构成一棵树。这棵树从一个任意的根结点r开始，一直长大到覆盖V中的所有结点时为止。算法每一步在连接集合A和A之外的结点的所有边中，选择一条权值最小的边加入进行计算。本策略也属于贪心策略，因为每一步所加入的边都必须是使树的总权重增加量最小的边。(逐步连接)

最短路径

• 最短路径问题：从在带权有向图(无向图也可以)G中某一顶点出发，找出一条通往另一个顶点的最短路径，最短也就是沿路径各边权值总和达到最小
• 最短路径算法：
  1. 单源最短路径--Dijkstra算法：针对一个带权有向图G，将所有结点分为两组S和Q，S是已经确定最短路径的结点集合，在初始时为空(可以放入初始点s)，Q为其余未确定最短路径的结点集合，每次从Q中找出一个起点到该结点代价最小的结点u，将u从Q 中移出，并放入S中，对u的每一个相邻结点v进行松弛操作。松弛即对每一个相邻结点v，判断源节点s到结点u的代价与u 到v的代价之和是否比原来s到v的代价更小，若代价比原来小则要将s到v的代价更新为s到u与u到v的代价之和，否则维持原样【试能不能找到更短的路径】。如此一直循环直至集合Q为空，即所有节点都已经查找过一遍并确定了最短路径，至于一些起点到达不了的结点在算法循环后其代价仍为初始设定的值，不发生变化。Dijkstra算法每次都是选择V-S中最小的路径节点来进行更新，并加入S中，所以该算法使用的是贪心策略(局部贪心)【问题是不支持图中带负权路径(因为可能绕路之后使路径更短了)，如果带有负权路径，则可能找不到一些路径的最短路径】(每次只确定一个节点，保证了该路径是当时的最短路径)
  2. 单源最短路径--Bellman-Ford算法：bellman-ford算法可以解决负权图的单源最短路径问题。它的优点是可以解决有负权边的单源最路径问题，而且可以用来判断是否有负权回路。它也有明显的缺点，它的时间复杂度*O(NE)(N是点数，E是边数)普遍是要高于Diikstra算法O(N^2^)的。像这里如果我们使用邻接矩阵实现，那么遍历所有边的数量的时间复杂度就是O(N^3^)（都要遍历），这里也可以看出来Bellman-Ford就是一种暴力求解更新【可以解决负权路径，但是解决不了负权回路(回路权和为负数，负权回路不存在最短路径)】【可以检测负权回路】(每次都选的都是最小路径，所以没选到的路径不需要考虑**)
  3. 多源最短路径--Floyd-Warshall算法：使用了动态规划的原理，适合用于求带负权路径的图中的任意两点之间的最短路径问题(不带负权路径还是Dijkstra算法更好)

核心代码⚙️

#include "DisjiontSet.h"
#define MAX_INT INT_MAX

// 使用邻接矩阵实现图
namespace Matrix
{
    // TODO:W:权值(带权图每条边都有对应的权值);Direction:表示该图是否有方向,MAX_W表示两个顶点不相连时边的缺省值
    template<class V, class W, W MAX_W = MAX_INT, bool Direction = false>
    class Graph
    {
        typedef Graph<V, W, MAX_W, Direction> Self;
    public:

        Graph() = default;

        // 图的创建
        // 1.IO输入 ---- 不方便写侧式,不过OJ中适合
        // 2.图的结构关系写在文件中,使用输入输出流读取文件
        // 3.手动添加边 ---- 方便测试和修改
        Graph(const V* a, size_t n) // 传n个V数据组成的数组
        {
            if (a  nullptr && n > 0) 
            {
                throw std::invalid_argument("Null pointer with non-zero size");
            }

            _vertexs.reserve(n);
            _matrix.resize(n);
            for (size_t i = 0; i < n; i++)
            {
                _vertexs.push_back(a[i]);
                _indexMap[a[i]] = i;

                _matrix[i].resize(n, MAX_W);
            }
        }

        // 获取顶点的索引值
        int GetVertexIndex(const V& value)
        {
            // 检查这个顶点是否存在(不使用operator[]的原因是因为当这个顶点不存在时会自动插入键为V的元素)
            auto it = _indexMap.find(value);
            if (it != _indexMap.end())
            {
                return it->second;
            }
            else
            {
                // 抛出异常
                throw std::invalid_argument("nonexistent value");
                return -1;
            }
        }

        // 添加边(src:源数据,dst:目标数据)
        void AddEdge(const V& src, const V& dst, const W& w)
        {
            if (src  dst)
            {
                // 抛出异常
                throw std::invalid_argument("src is the same as dst");
                return;
            }

            int srci = _indexMap[src];
            int dsti = _indexMap[dst];

            _AddEdge(srci, dsti, w);
        }

        // 广度优先遍历
        void BFS(const V& src)
        {
            // 使用队列实现BFS
            int srci = GetVertexIndex(src);
            queue<int> q; // 建立队列储存节点索引值
            vector<bool> visited(_vertexs.size(), false);
            int SizeInLevel = 1; // 每层元素的个数
            p.push_back(srci);
            visited[srci] = true;
            while (!q.empty())
            {
                for (int i = 0; i < SizeInLevel; ++i)
                {
                    int front = q.front();
                    cout << front << ":" << _vertexs[front] << " ";
                    for (int j = 0; j < _vertexs.size(); ++j)
                    {
                        // 将相邻未入队的元素插入队
                        if (_matrix[front][j] != MAX_W && visited[j] != true)
                        {
                            q.push(j);
                            visited[j] = true;
                        }
                    }
                    q.pop();
                }
            }
            cout << endl;
        }

        // 深度优先遍历(适用于连通图)
        void DFS(const V& src)
        {
            // 图是很容易过深的数据结构,所以到一定程度了DFS也不适合图使用
            size_t srci = GetVertexIndex(src);
            vector<bool> visited(_vertexs.size(), false);
            _DFS(srci, visited);
            cout << endl;
        }

        // 为了辅助完成最小生成树的构建,我们创建一个Edge结构体
        struct Edge
        {
            size_t _srci;
            size_t _dsti;
            W _w;

            Edge(size_t srci, size_t dsti, const W& w)
                : _srci(srci)
                , _dsti(dsti)
                , _w(w)
            {

            }

            // const保证在该函数中不能修改类成员且支持const对象访问(只读)
            bool operator>(const Edge& e) const
            {
                return this->_w > e._w;
            }
        };

        #pragma region 最小生成树(无向图)
        // 最小生成树:要求函数返回最小生成树以及最小生成树的权和
        // 最小生成树--Kruskal算法
        W Kruskal(Self& minTree)
        {
            size_t vertexSize = _vertexs.size();
            // 1.对minTree进行初始化
            minTree._vertexs = _vertexs;
            minTree._indexMap = _indexMap;
            minTree._matrix.resize(vertexSize);

            for (int i = 0; i < vertexSize; i++)
            {
                minTree._matrix[i].resize(vertexSize, MAX_W);
            }

            // 2.设置一个优先级队列用来储存每条边(方便后续的添加)
            priority_queue<Edge, vector<Edge>, greater<Edge>> minpq; // TODO:构造一个小根堆优先级队列,让边权值小的放在前面
            for (int i = 0; i < vertexSize; ++i)
            {
                // TODO:标记
                for (int j = 0; j < vertexSize - i; ++j)
                {
                    // 只探测左上角的元素
                    if (i < j && _matrix[i][j] != MAX_W)
                    {
                        minpq.push(Edge(i, j, _matrix[i][j]));
                    }
                }
            }

            // 3.要选出vertexSize-1条边,要设置一个并查集用来检测两个节点是否已选择连接
            DisjiontSet DjSet(vertexSize);
            W totalW = W();
            int size = 0;
            while (!minpq.empty())
            {
                // 取队顶
                Edge min = minpq.top();
                minpq.pop();
                if (!DjSet.InSet(min._srci, min._dsti))
                {
                    cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;
                    minTree.AddEdge(min._srci, min._dsti, min._w);

                    totalW += min._w;
                    DjSet.Union(min._srci, min._dsti);
                    ++size;
                }
            }

            // 4.节点连接完毕,查看图是否联通
            if (size  vertexSize - 1)
            {
                return totalW;
            }
            else
            {
                throw std::invalid_argument("Graph doesn't connected");
                return V();
            }
        }

        // 最小生成树--Prim算法
        W Prim(Self& minTree, const V& src)
        {
            size_t srci = GetVertexIndex(src);
            size_t vertexSize = _vertexs.size();
            // 1.对minTree进行初始化
            minTree._vertexs = _vertexs;
            minTree._indexMap = _indexMap;
            minTree._matrix.resize(vertexSize);

            for (int i = 0; i < vertexSize; i++)
            {
                minTree._matrix[i].resize(vertexSize, MAX_W);
            }

            vector<bool> X(vertexSize, false);
            X[srci] = true;

            // 2.设置一个优先级队列用来储存每条边(方便后续的添加)
            priority_queue<Edge, vector<Edge>, greater<Edge>> minpq; // TODO:构造一个小根堆优先级队列,让边权值小的放在前面
            for (int i = 0; i < vertexSize; ++i)
            {
                minpq.push(Edge(srci, i, _matrix[srci][i])); // 将集合X与非X中的所有相邻边插入优先级队列中
            }

            size_t size = 0;
            W totalW = W();
            while (!minpq.empty() && size < vertexSize - 1)
            {
                Edge min = minpq.top();
                minpq.pop();
                // 如果dsti也在集合X.true中,那么成环
                if (X[min._dsti]) 
                {
                    continue;
                }

                cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;
                minTree._AddEdge(min._srci, min._dsti, min._w);
                X[min._dsti] = true;
                totalW += min._w;
                ++size;

                // 将新加入集合的_dsti相邻非X.true的边插入minpq队列中
                for (int i = 0; i < vertexSize; ++i)
                {
                    if (X[i]  false && _matrix[min._dsti][i] != MAX_W)
                    {
                        minpq.push(Edge(min._dsti, i, _matrix[min._dsti][i]));
                    }
                }
            }

            if (size  vertexSize - 1)
            {
                return totalW;
            }
            else
            {
                return W();
            }
        }
        #pragma endregion

        #pragma region 最短路径

        // 将源点到图中其他点的最短路径打印出来
        void PrintShortPath(const int& srci, const vector<W>& dist, const vector<int>& pPath)
        {
            int vertexSize = _vertexs.size();
            for (int i = 0; i < vertexSize; i++)
            {
                vector<int> path;
                if (i  srci) // 不打印自身到自身的距离
                {
                    continue;
                }

                int parent = i;
                while (parent != srci)
                {
                    path.push_back(parent);
                    parent = pPath[parent];
                } 
                path.push_back(srci); // 最后把起点插入

                reverse(path.begin(), path.end());
                for (auto e : path)
                {
                    cout << _vertexs[e] << "->";
                }
                cout << ": " << dist[i] << endl;
            }
        }

        /// <summary>
        /// 单源最短路径--Dijkstra算法
        /// </summary>
        /// <param name="src">:即为源节点</param>
        /// <param name="dist">:为源节点到对应节点的路径权和</param>
        /// <param name="pPath">:对应位置节点的上一个节点</param>
        void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath)
        {
            int srci = GetVertexIndex(src);
            int vertexSize = _vertexs.size();
            dist.resize(vertexSize, MAX_W); // TODO:对dist数组进行初始化,默认源节点到每个节点的距离为无限长
            pPath.resize(vertexSize, -1); // TODO:对pPath数组进行初始化,默认每个节点没有上一个节点(TODO:这个数组是为了方便最小路径的遍历的,最小路径的生成不需要这个数组)

            dist[srci] = W(); // 自身到自身的距离为对应变量的缺省值
            pPath[srci] = srci; // 源节点的上一个节点置为自身

            vector<bool> Traveled(vertexSize, false); // 集合Traveled用于表示节点是否已经产生了"最小距离"

            // 需要遍历size次,保证每个节点都被访问了
            for (int j = 0; j < vertexSize; ++j)
            {
                // 1.选择上一次松弛操作后确定的最小路径和最小路径节点
                int minI = srci;
                W minW = MAX_W;
                for (int i = 0; i < vertexSize; ++i)
                {
                    // 选出最小点与最小路径
                    if (Traveled[i]  false && dist[i] < minW)
                    {
                        minI = i;
                        minW = dist[i];
                    }
                }

                // 将最短路径节点更新
                Traveled[minI] = true;

                // 2.进行松弛操作(TODO:计算新的最小距离点与相邻的点的距离)
                for (int i = 0; i < vertexSize; i++)
                {
                    if (Traveled[i]  false && _matrix[minI][i] != MAX_W && _matrix[minI][i] + minW < dist[i])
                    {
                        dist[i] = _matrix[minI][i] + minW; // 将最短路径备选案存在dist数组中
                        pPath[i] = minI;
                    }
                }
            }
            PrintShortPath(srci, dist, pPath);
        }

        // 单源最短路径--bellmanFord算法
        bool bellmanFord(const V& src, vector<W>& dist, vector<int>& pPath)
        {
            int srci = GetVertexIndex(src);
            int vertexSize = _vertexs.size();
            dist.resize(vertexSize, MAX_W);
            pPath.resize(vertexSize, -1);

            dist[srci] = W();

            // 进行size轮能保证极端情况也能遍历完(但是数据不更新就说明已经遍历完了)
            for (int k = 0; k < vertexSize; ++k)
            {
                bool Update = false; // 不更新代表负权边也处理完了
                // 将每个点的距离都进行一次更新
                for (int i = 0; i < vertexSize; ++i)
                {
                    for (int j = 0; j < vertexSize; ++j)
                    {
                        // 距离比原来小,更新
                        if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
                        {
                            Update = true;
                            dist[j] = dist[i] + _matrix[i][j];
                            pPath[j] = i;
                        }
                    }
                }
                // 不更新了说明数据处理完毕
                if (!Update)
                    return true;
            }

            // 如果上面的vertexSize都遍历完后再遍历一次还会更新的话,说明有负权回路,需要处理
            for (size_t i = 0; i < vertexSize; i++)
            {
                for (size_t j = 0; j < vertexSize; j++)
                {
                    // 测试还会不会更新
                    if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
                    {
                        return false; // 说明有负权回路
                    }
                }
            }

            return true;
        }

        // 多源最短路径--FloydWarShall算法(无负权回路可使用Dijkstra算法,效率更高)
        void FloydWarShall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath)
        {
            int vertexSize = _vertexs.size();
            vvDist.resize(vertexSize);
            vvpPath.resize(vertexSize);

            for (size_t i = 0; i < vertexSize; i++)
            {
                vvDist[i].resize(n, MAX_W);
                vvpPath[i].resize(n, -1);
            }

            // 给每个源节点到自身的距离一个初值
            for (size_t i = 0; i < vertexSize; i++)
            {
                for (size_t j = 0; j < vertexSize; j++)
                {
                    if (_matrix[i][j] != MAX_W)
                    {
                        vvDist[i][j] = _matrix[i][j];
                        vvpPath[i][j] = i;
                    }

                    if (i  j)
                    {
                        vvDist[i][j] = 0;
                        vvpPath[i][j] = i;
                    }
                }
            }

            // 跟BellmanFord算法一样,都要更新N次,不过是每个节点同时更新,而不是一个节点单独更新
            for (int k = 0; k < vertexSize; ++k)
            {
                for (int i = 0; i < vertexSize; ++i)
                {
                    for (int j = 0; j < vertexSize; ++j)
                    {
                        // 如果i->k,k->j的距离已经存在,且是更短路径,那么就更新这个路径
                        if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W && vvDist[i][k] + vvDist[k][j] < vvDist[i][j])
                        {
                            vvDist[i][j] = vvDist[i][k] + vvDist[k][j];
                            // 因为i->k->j是通路了,所以vvpPath[k][j]表示的就是i->j路径下j的上一个顶点(pPath)
                            vvpPath[i][j] = vvpPath[k][j];
                        }
                    }
                }
            }
        }
        #pragma endregion

        // 将图打印出来
        void Print()
        {
            // 顶点
            for (size_t i = 0; i < _vertexs.size(); ++i)
            {
                cout << "[" << i << "] ->" << _vertexs[i] << endl;
            }
            cout << endl;

            // 横向下标
            cout << "\\ ";
            for (size_t i = 0; i < _vertexs.size(); ++i)
            {
                printf("%4d", i);
            }
            cout << endl;

            // 矩阵
            for (size_t i = 0; i < _matrix.size(); ++i)
            {
                // 竖向下标
                cout << i << " ";
                for (size_t j = 0; j < _matrix[i].size(); ++j)
                {
                    if (_matrix[i][j]  MAX_W)
                        printf("%4c", '*');
                    else
                        printf("%4d", _matrix[i][j]);
                }
                cout << endl;
            }
        }
    private:
        // _vertexs储存的V数据,通过_indexMap映射为int类型,再通过int来访问_matrix或_vertexs
        vector<V> _vertexs; // 储存顶点的集合
        map<V, int> _indexMap; // 将顶点统一映射为整型的map
        vector<vector<W>> _matrix; // 邻接矩阵

        void _AddEdge(int srci, int dsti, const W& w)
        {
            _matrix[srci][dsti] = w;
            if (!Direction)
            {
                _matrix[dsti][srci] = w;
            }
        }

        // 递归子函数
        void _DFS(int srci, vector<bool>& visited)
        {
            // 基础操作
            cout << srci << ":" << _vertexs[srci] << " ";
            visited[srci] = true;

            // 使用循环确定一下srci的连接情况
            for (int i = 0; i < _vertexs.size(); ++i)
            {
                if (_matrix[srci][i] != MAX_W && !visited[i])
                {
                    _DFS(i, visited);
                }
            }
        }
    };
}

// 使用邻接表实现图
namespace LinkTable
{

}

• 部分代码的邻接矩阵实现：

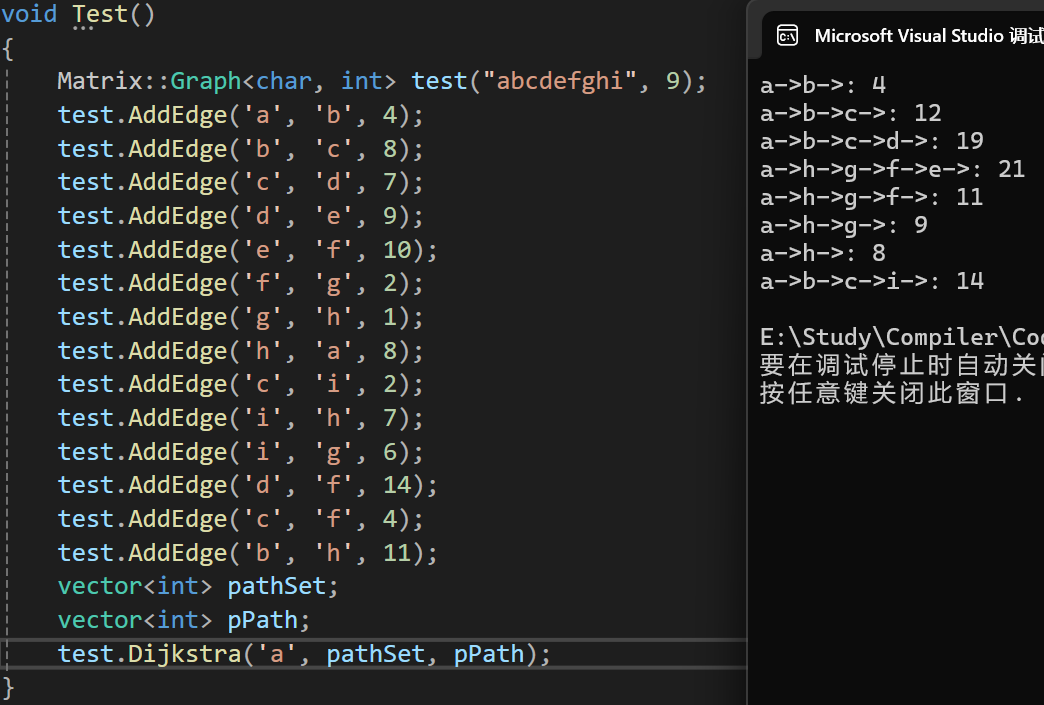
图算法复杂度分析🎯

算法	时间复杂度	空间复杂度	适用场景
DFS/BFS	O(V+E)	O(V)	图遍历、连通性检测
Dijkstra	O((V+E)logV)	O(V)	非负权最短路径
Bellman-Ford	O(VE)	O(V)	含负权最短路径
Floyd-Warshall	O(V³)	O(V²)	所有顶点对最短路径
Prim	O((V+E)logV)	O(V)	最小生成树
Kruskal	O(ElogE)	O(V)	最小生成树

总结：图的优势与应用💡

优势	说明
强大的建模能力	能表示现实世界中任意复杂的关系网络
丰富的算法支持	拥有大量成熟的图论算法
灵活性	支持有向/无向、带权/无权等多种变体
可扩展性	易于添加新的顶点和边

• 实际应用场景

1. 社交网络分析
   • 场景：好友推荐、影响力分析、社区发现
   • 算法：PageRank、标签传播、连通分量
   • 规模：处理数十亿顶点和边的超大规模图
2. 路径规划与导航
   • 场景：GPS导航、物流配送、网络路由
   • 算法：Dijkstra、A*、Floyd-Warshall
   • 需求：实时计算最短或最优路径
3. 推荐系统
   • 场景：商品推荐、内容推荐、好友推荐
   • 技术：图神经网络、随机游走
   • 优势：利用用户-物品的复杂交互关系
4. 知识图谱
   • 场景：搜索引擎、智能问答、语义网
   • 结构：实体作为顶点，关系作为边
   • 应用：Google知识图谱、医疗知识库
5. 电路设计
   • 场景：PCB布线、逻辑电路优化
   • 算法：最小生成树、欧拉路径
   • 挑战：满足物理约束的优化布局
6. 编译器设计
   • 场景：控制流图、数据流分析、寄存器分配
   • 应用：代码优化、死代码消除
7. 生物信息学
   • 场景：蛋白质相互作用网络、基因调控网络
   • 分析：网络中心性、模块检测
8. 网络安全
   • 场景：攻击图分析、异常检测
   • 技术：图模式匹配、社区发现

3.4跳表

• 概念与特征：跳表（Skip List）是一种概率性的查找型数据结构，通过在有序链表上建立多级索引来实现近似二分查找的高效操作。它结合了链表的灵活性和数组的快速查找优势，是平衡树的高效替代方案。

设计多层链表

原理设计

• 让每相隔两个节点(链表节点)升高一层，增加一个指针，让指针指向下一个节点。这样所有新增加的指针连成了一个新的链表，但它包含的节点个数只有原来的一半。由于新增加的指针，我们不需要与链表中每个节点逐个进行比较了，需要比较的节点数只有原来的一半

  • 比较思路：先从高层链表开始查找并比较，如数据比下一个节点的数据大，就跳到下一个节点；若是比下一个节点的数据小，就往下降一层链表，然后再和它的下一个节点数据对比，以此往复知道找到指定数据为止【先比较高层链表可以大大减少搜索次数】

  • 可能存在的问题：skiplist正是受这种多层链表的想法的启发下而设计出来的数据结构，实际上，按照上面的链表生成方式，上面每一层链表的节点个数，是下面一层链表的节点个数的一半，这样的查找过程就非常类似于二分查找，使得查找的时间复杂度可以降低至O(logN)。但是这个结构在插入删除数据时有很大的问题，插入或删除一个节点之后，就会打破上下两层链表之间节点个数按照严格的2：1的对应关系。如果想要维持这种对应关系，就需要把插入或删除位置后面的所有节点重新进行调整(也包括新插入的节点)，这会让时间复杂度重新退化为O(N)

优化设计

• skiplist的设计为了避免出现上述存在的问题，做了一个很大胆的处理，不再要求相邻两层链表中的节点个数得严格按照比例关系，而是插入一个节点的时候随机出一个层数值(就是节点的层数是随机分配的)，这样每次插入和删除时就不需要考虑其他节点的层数，这样就好处理多了。细节如下图【即一个节点有几层其实是随机的】

  • 随机分配的伪代码：

  

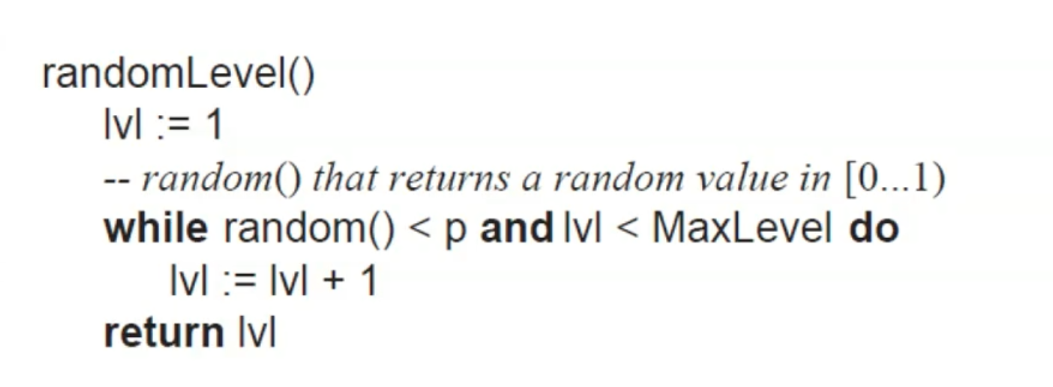
核心代码⚙️

#pragma once
#include <iostream>
#include <vector>
#include <time.h>
#include <random>
#include <chrono>
using namespace std;

struct SkipListNode
{
    int _val;
    vector<SkipListNode*> _nextV;

    SkipListNode(int value, int level)
        : _val(value)
        , _nextV(level, nullptr)
    { }
};

class SkipList
{
    typedef SkipListNode Node;
public:
    SkipList()
        : _maxlevel(32)
        , _p(0.25)
    {
        srand(time(0)); // 在构造时生成随机数
        _head = new Node(-1, 1);
    }

    bool Search(int value)
    {
        Node* cur = _head;
        int highI = _head->_nextV.size() - 1;
        while (highI >= 0)
        {
            // 如果下一个位置的值存在且值比value小,那么cur往后移动
            if (cur->_nextV[highI] && cur->_nextV[highI]->_val < value)
            {
                cur = cur->_nextV[highI];
            }
            else if(cur->_nextV[highI] && cur->_val < value)
            {
                --highI;
            }
            else
            {
                return true; // 找到了
            }
        }
        return false; // 跳出了依然没找到,说明不存在该值
    }

    void add(int value)
    {
        int level = RandomLevel();
        Node* newNode = new Node(value, level);

        // TODO:设置一个prevV数组用来记录newNode每层中的上一个节点
        vector<Node*> prevV = FindPrevNodeSet(value);

        // 检查层数是否比之前的最高层数还高
        if (level > _head->_nextV.size())
        {
            _head->_nextV.resize(level, nullptr);
            // 当前的最高高度超出了prevV的层数
            prevV.resize(level, _head); // 将超出层数的前驱设置为_head
        }

        // 建立link
        for(int i = 0; i < level; ++i)
        {
            newNode->_nextV[i] = prevV[i]->_nextV[i];
            prevV[i]->_nextV[i] = newNode;
        }
    }

    bool Erase(int value)
    {
        vector<Node*> prevV = FindPrevNodeSet(value);

        // 无借足够的节点来删除,或者没有对应关键字的节点
        if (prevV[0]->_nextV[0]  nullptr || prevV[0]->_nextV[0]->_val != value)
        {
            return false;
        }

        Node* del = prevV[0]->_nextV[0];
        // 删除相邻关系
        for (size_t i = 0; i < del->_nextV.size(); ++i)
        {
            prevV[i]->_nextV[i] = del->_nextV[i];
        }
        delete del;
        return true;
    }

    vector<Node*> FindPrevNodeSet(int value)
    {
        int highI = _head->_nextV.size() - 1;
        // 将prevV数组的高度设置为当前最高
        vector<Node*> prevV(highI + 1, nullptr);

        Node* cur = _head;
        while (highI >= 0)
        {
            if (cur->_nextV[highI] && cur->_nextV[highI]->_val < value)
            {
                cur = cur->_nextV[highI];
            }
            else if (cur->_nextV[highI]  nullptr || cur->_nextV[highI]->_val >= value)
            {
                prevV[highI] = cur;
                // 开始寻找下一层的prev节点
                --highI;
            }
        }

        return prevV;
    }

private:
    Node* _head;
    size_t _maxlevel; // 这个跳表理论上的最高层树
    double _p; // 每次有_p的概率增加一层

    // 用于生成随机层树的函数
    int RandomLevel()
    {
        static default_random_engine generator(chrono::system_clock::now().time_since_epoch().count());
        static std::uniform_real_distribution<double> distribution(0.0, 1.0); // 将给予的值映射分配到(0.0, 1.0)这个区域上
        size_t level = 1;
        while (distribution(generator) <= _p && level < _maxlevel)
        {
            ++level;
        }

        return level;
    }
};

总结：跳表的优势与应用💡

优势	说明
实现简单	比平衡树更容易实现和调试
性能优秀	平均情况下与平衡树相当
支持并发	易于实现线程安全版本
范围查询	天然支持高效的范围查询

• 适用场景

1. 需要快速查找和范围查询
   • 数据库索引
   • 缓存系统
2. 需要简单实现
   • 原型开发
   • 教学演示
   • 实时游戏排行榜
3. 需要高并发
   • 多线程环境
   • 分布式系统